
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于点A,B(1,0),与
与x轴交于点A,B(1,0),与![]() 轴交于点C(0,3),对称轴为直线
轴交于点C(0,3),对称轴为直线![]() .
.
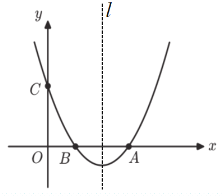
(1)求抛物线的解析式及点A的坐标;
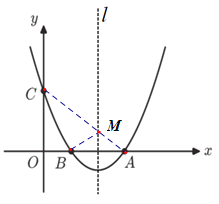
(2)在对称轴![]() 上是否存在一点M,使得△BCM周长最小?若存在,求出△BCM周长;若不存在,请说明理由;
上是否存在一点M,使得△BCM周长最小?若存在,求出△BCM周长;若不存在,请说明理由;
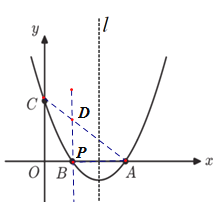
(3)若点P是抛物线上一动点,从点C沿抛物线向点A运动,过点P作PD//![]() 轴,交AC于点D,当△ADP是直角三角形时,求点P的坐标.
轴,交AC于点D,当△ADP是直角三角形时,求点P的坐标.
【答案】(1)y=x2﹣4x+3;(2)存在,![]() ;(3)P(1,0)或(2,-1)
;(3)P(1,0)或(2,-1)
【解析】
(1)用待定系数法求解即可;
(2)连接AC交直线![]() 于点M,连接BM.由轴对称的性质可知此时BM+MC=AM+MC=AC,即△ABM周长最短;
于点M,连接BM.由轴对称的性质可知此时BM+MC=AM+MC=AC,即△ABM周长最短;
(3)分当∠APD=90°时和当∠PAD=90°时两种情况求解即可.
解:(1)将B(1,0),C(0,3)代入![]() 中,得
中,得
![]() ,解得
,解得![]() ,
,
∴抛物线解析式为y=x2﹣4x+3;
(2)存在.
连接AC交直线![]() 于点M,连接BM.
于点M,连接BM.
∵点A,B关于直线![]() 对称,
对称,
∴BM=CM,
∴BM+MC=AM+MC=AC,
∴此时△ABM周长最短.
∵![]() ,
,
∴△ABM的周长最小为AC+BC=![]() ;
;
(3)由题得,A(3,0),B(1,0),C(0,3),
∴OA=OC ,∴∠CAO=45°,
当∠APD=90°时,∵PD//y轴,AB⊥y轴,
∴PD⊥AB,∴点P与点B重合,
∴P点坐标为(1,0);
当∠PAD=90°时,则∠PAB=∠DAB=45°,
∵AB⊥PD,∴![]() ,
,
设直线AC的解析式为y=kx+b,
把A(3,0), C(0,3)代入得
![]() ,
,
解得
![]() ,
,
∴直线AC的解析式为y=-x+3,
设点D(m,-m+3),点P(m,m2﹣4m+3),
∴![]() ,解得
,解得![]() (舍去),
(舍去),
∴P点坐标为(2,-1),
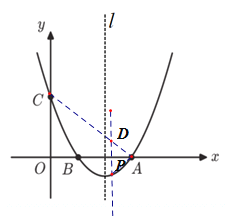
综上所述,P(1,0)或(2,-1).


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AG⊥BC,垂足为点G,点E为边AC上一点,BE=CE,点D为边BC上一点,GD=GB,连接AD交BE于点F.
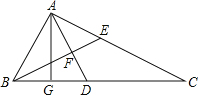
(1)求证:∠ABE=∠EAF;
(2)求证:AE2=EFEC;
(3)若CG=2AG,AD=2AF,BC=5,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组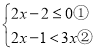
请结合题意填空,完成本题的解答
(1)解不等式①,得___________;
(2)解不等式②,得___________;
(3)把不等式①和②的解集在数轴上表示出来:
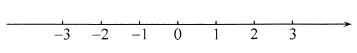
(4)原不等式组的解集为_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,
,![]()
(1) 将![]() 向右平移6个单位长度至
向右平移6个单位长度至![]() , 再将
, 再将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 至
至![]() ,请按要求画出图形;
,请按要求画出图形;
(2)在![]() 的变换过程中,直接写出点
的变换过程中,直接写出点![]() 的运动路径长
的运动路径长
(3)![]() 可看成
可看成![]() 绕某点
绕某点![]() 旋转
旋转![]() 得到的, 则点
得到的, 则点![]() 的坐标为
的坐标为

查看答案和解析>>
科目:初中数学 来源: 题型:
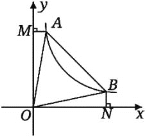
【题目】如图,直线![]() 与双曲线
与双曲线![]() 交于A、B两点,连接OA、OB,
交于A、B两点,连接OA、OB,![]() 轴于点M,
轴于点M,![]() 轴于点N,有以下结论:①
轴于点N,有以下结论:①![]() ;②
;②![]() ;③
;③![]() 则
则![]() ;④当
;④当![]() 时,
时,![]() .其中结论正确的是___________
.其中结论正确的是___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O在∠APB的平分线上,⊙O与PA相切于点C.
(1)求证:直线PB与⊙O相切;
(2)PO的延长线与⊙O交于点E.若⊙O的半径为3,PC=4.求弦CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在小正方形的边长均为l的方格纸中,有线段AB,BC.点A,B,C均在小正方形的顶点上.
(1)在图1中画出四边形ABCD,四边形ABCD是轴对称图形,点D在小正方形的项点上:
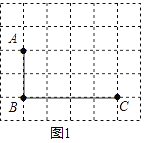
(2)在图2中画四边形ABCE,四边形ABCE不是轴对称图形,点E在小正方形的项点上,∠AEC=90°,EC>EA;直接写出四边形ABCE的面积为________.
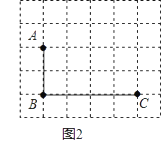
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市特产大闸蟹,2016年的销售额是![]() 亿元,因生态优质美誉度高,销售额逐年增加2018年的销售额达
亿元,因生态优质美誉度高,销售额逐年增加2018年的销售额达![]() 亿元,若2017、2018年每年销售额增加的百分率都相同.
亿元,若2017、2018年每年销售额增加的百分率都相同.
(1)求平均每年销售额增加的百分率;
(2)该市这![]() 年大闸蟹的总销售额是多少亿元?
年大闸蟹的总销售额是多少亿元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图所示直线y=kx+2(k≠0)与反比例函数y=![]() (m≠0)分别交于点P,与y轴、x轴分别交于点A和点B,且cos∠ABO=
(m≠0)分别交于点P,与y轴、x轴分别交于点A和点B,且cos∠ABO=![]() ,过P点作x轴的垂线交于点C,连接AC,
,过P点作x轴的垂线交于点C,连接AC,
(1)求一次函数的解析式.
(2)若AC是△PCB的中线,求反比例函数的关系式.
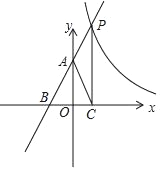
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com