Question

4．如图1，等腰Rt△ABC，AC=BC=4，D为BC中点，矩形BFEG，EF=4，BF=8，且F、B、C共线．△ABD沿BF运动，速度为每秒1个单位长，运动中记为△A₁B₁D₁．当A₁与E重合时，运动停止运动过程中△A₁B₁D₁与△BEF重叠部分面积记为S．
（1）当线段A₁D₁过线段EB中点时，求运动时间t；
（2）求S与t的关系式；
（3）取线段BF中点为H，连接EH，如图2，当B₁与F重合时，将∠A₁B₁D₁绕点F旋转，射线B₁A₁与直线EH交于M，射线B₁D₁与直线EH交于N，若EM：MN=3：5，求线段EM的长．

Answer 1

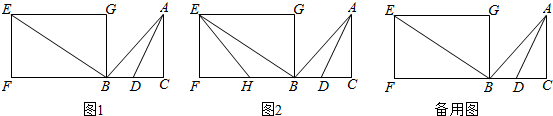
分析 （1）过O作MN⊥EG于M，交BF于N，分别计算出BN、B₁D₁、D₁N的长，则可求出BB₁的长，即t的值；
（2）分五种情况进行讨论：①当0≤t≤2时，如图2，重叠部分是△BCB₁，作高CD，根据同角的三角函数列式表示出高CD的长，利用面积公式求出S与t的关系式；
②当2＜t≤8时，如图3，重叠部分是四边形CB₁D₁M，重叠部分面积是两三角形面积的差；
③当8＜t≤10时，如图4，重叠部分是五边形CQFD₁M，重叠部分面积S=${S}_{△B{B}_{1}C}$-${S}_{△{D}_{1}MB}$-${S}_{△{B}_{1}FQ}$，代入计算即可；
④当10＜t＜12时，如图5，重叠部分是四边形CPQM，S=${S}_{△B{B}_{1}C}$-${S}_{△{D}_{1}MB}$-${S}_{△{B}_{1}FP}$+${S}_{△{D}_{1}QF}$，代入计算即可；
⑤当t=12时，如图6，S=0；
（3）∠A₁B₁D₁绕点F旋转，发现在旋转过程中，交点N与H重合，所以有两种情况：①如图7，当交点M在线段EH上时，求出EH的长，再按已知的比得出结论：EM=$\frac{3}{8}$EH=$\frac{3}{8}$×$4\sqrt{2}$=$\frac{3\sqrt{2}}{2}$；
②如图8，当交点M在直线EH上时，同理得EM=6$\sqrt{2}$．

解答 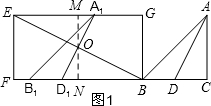解：（1）如图1，线段A₁D₁过线段EB中点O，
过O作MN⊥EG于M，交BF于N，
∵四边形EFBG是矩形，
∴EG∥FB，
∴MN⊥BF，
∵△ABC是等腰直角三角形，D为BC中点，
∴BD=DC，
∵AC=BC=4，
∴BD=DC=2，
由勾股定理得：AD=$\sqrt{A{C}^{2}+D{C}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$，
∵EG∥FB，
∴∠GEB=∠EBF，
∵EO=OB，∠EOA₁=∠BOD₁，
∴△EOA₁≌△BOD₁，
∴A₁O=D₁O=$\frac{1}{2}$A₁D₁=$\frac{1}{2}$AD=$\frac{1}{2}$×2$\sqrt{5}$=$\sqrt{5}$，
同理：OM=ON=$\frac{1}{2}$MN=$\frac{1}{2}$EF=2，
由勾股定理得：A₁M=$\sqrt{O{{A}_{1}}^{2}-O{M}^{2}}$=$\sqrt{（\sqrt{5}）^{2}-{2}^{2}}$=1，
同理D₁N=1，
∵EO=OB，ON∥EF，
∴FN=BN=$\frac{1}{2}$BF=4，
∴BB₁=B₁D₁+D₁N+BN=2+1+4=7，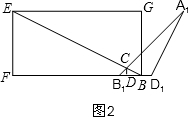
∴t=7，
则当线段A₁D₁过线段EB中点时，运动时间t为7秒；
（2）分五种情况讨论：
①当0≤t≤2时，如图2，重叠部分是△BCB₁，
过C作CD⊥BF于D，
∵∠A₁B₁D₁=45°，
∴CD=B₁D，
tan∠EBF=$\frac{CD}{BD}=\frac{EF}{BF}$=$\frac{4}{8}$=$\frac{1}{2}$，
∴CD=$\frac{1}{2}$BD=$\frac{1}{2}$（BB₁-CD，
$\frac{3}{2}$CD=$\frac{1}{2}$t，
CD=$\frac{1}{3}$t，
∴S=${S}_{△B{B}_{1}C}$=$\frac{1}{2}$BB₁•CD=$\frac{1}{2}t$•$\frac{1}{3}t$=$\frac{1}{6}{t}^{2}$；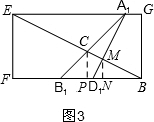
②当2＜t≤8时，如图3，重叠部分是四边形CB₁D₁M，
分别过C、M向BF作垂线CP和MN，垂足分别为P、N，
由平移得如图1：∠A₁D₁B=∠ADC，
tan∠A₁D₁B=$\frac{MN}{{D}_{1}N}$=$\frac{AC}{CD}$=$\frac{4}{2}$=2，
∴D₁N=$\frac{1}{2}$MN，
∵DD₁=t，BD=2，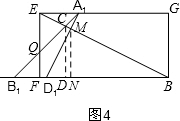
∴D₁B=DD₁-BD=t-2，
tan∠EBF=$\frac{MN}{BN}$=$\frac{1}{2}$，
2MN=t-2-$\frac{1}{2}$MN，
MN=$\frac{2}{5}$（t-2），
由①得：CP=$\frac{1}{3}$t，
∴S=${S}_{△B{B}_{1}C}$-${S}_{△{D}_{1}MB}$，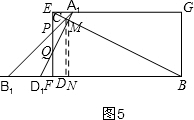
=$\frac{1}{2}$BB₁•CP-$\frac{1}{2}$BD₁•MN，
=$\frac{1}{2}$t•$\frac{1}{3}t$-$\frac{1}{2}$（t-2）•$\frac{2}{5}$（t-2），
=-$\frac{1}{30}{t}^{2}$+$\frac{4}{5}$t-$\frac{4}{5}$；
③当8＜t≤10时，如图4，重叠部分是五边形CQFD₁M，则B₁F=t-8，
∵∠A₁B₁F=45°，
∴△FB₁Q是等腰直角三角形，
∴FQ=B₁F=t-8，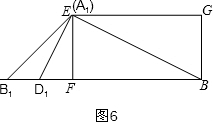
∴S=${S}_{△B{B}_{1}C}$-${S}_{△{D}_{1}MB}$-${S}_{△{B}_{1}FQ}$，
=-$\frac{1}{30}{t}^{2}$+$\frac{4}{5}$t-$\frac{4}{5}$-$\frac{1}{2}$B₁F•FQ，
=-$\frac{1}{30}{t}^{2}$+$\frac{4}{5}$t-$\frac{4}{5}$-$\frac{1}{2}$（t-8）（t-8），
=-$\frac{8}{15}$t²+$\frac{44}{5}t$-$\frac{164}{5}$；
④当10＜t＜12时，如图5，重叠部分是四边形CPQM，
∵BB₁=t，B₁D₁=2，BF=8，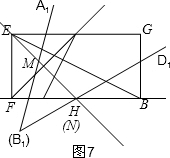
∴FD₁=t-2-8=t-10，B₁F=t-8，
∴PF=B₁F=t-8，$\frac{FQ}{F{D}_{1}}$=2，
∴FQ=2FD₁=2（t-10），
∴S=${S}_{△B{B}_{1}C}$-${S}_{△{D}_{1}MB}$-${S}_{△{B}_{1}FP}$+${S}_{△{D}_{1}QF}$，
=-$\frac{8}{15}$t²+$\frac{44}{5}t$-$\frac{164}{5}$+$\frac{1}{2}$（t-10）•2（t-10），
=$\frac{7}{15}{t}^{2}$-$\frac{56}{5}$t+$\frac{336}{5}$；
⑤当t=12时，如图6，S=0；
综上所述：S=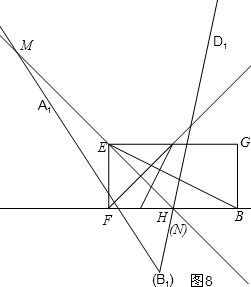$\left\{\begin{array}{l}{\frac{1}{6}{t}^{2}（0≤t≤2）}\\{-\frac{1}{30}{t}^{2}+\frac{4}{5}t-\frac{4}{5}（2＜t≤8）}\\{-\frac{8}{15}{t}^{2}+\frac{44}{5}t-\frac{164}{5}（8＜t≤10）}\\{\frac{7}{15}{t}^{2}-\frac{56}{5}t+\frac{336}{5}（10＜t＜12）}\\{0（t=12）}\end{array}\right.$
（3）有两种情况：①如图7，当交点M在线段EH上时，
∵H是BF的中点，
∴FH=4，
由勾股定理得：EH=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$，
∵EM：MN=3：5，EM+MN=EH，
∴EM=$\frac{3}{8}$EH=$\frac{3}{8}$×$4\sqrt{2}$=$\frac{3\sqrt{2}}{2}$，
②如图8，当交点M在直线EH上时，
∵EM：MN=3：5，EM+EH=MN，
∴EM=$\frac{4\sqrt{2}}{2}$×3=6$\sqrt{2}$，
综上所述：线段EM的长为$\frac{3\sqrt{2}}{2}$或6$\sqrt{2}$．

点评 本题是几何变换的综合题，考查了矩形、等腰直角三角形、全等三角形的性质和判定及旋转的性质，熟练掌握这些性质是做好本题的关键；同时，知道旋转前面的对应角相等；本题还利用了同角的三角函数列比例式表示线段的长，利用面积公式代入计算，求出对应的关系式；在计算重叠部分面积时，图形比较复杂，分情况讨论，此处容易丢解，因此要细心画图，准确找出重叠图形的各种类型．