
【题目】在Rt△ABC中,∠C=Rt∠,若BC:AC=3:4,BD平分∠ABC交AC于点D,则tan∠DBC的值为( )
A.![]()
B.![]()
C.![]()
D.![]()
科目:初中数学 来源: 题型:
【题目】已知:如图,以定线段AB为直径作半圆O,P为半圆上任意一点(异于A、B),过点P作半圆O的切线分别交过A、B两点的切线于D、C,连接OC、BP,过点O作OM∥CD分别交BC与BP于点M、N.下列结论:
①S四边形ABCD= ![]() ABCD;
ABCD;
②AD=AB;
③AD=ON;
④AB为过O、C、D三点的圆的切线.
其中正确的个数有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读完成问题:
数轴上,已知点A、B、C.其中,C为线段AB的中点:
(1)如图,点A表示的数为-1,点B表示的数为3,则线段AB的长为 , C点表示的数为 ;

(2)若点A表示的数为-1,C点表示的数为2,则点B表示的数为 ;
(3)若点A表示的数为t,点B表示的为t+2,则线段AB的长为 ,若C点表示的数为2,则t= ;
(4)点A表示的数为![]() ,点B表示的为
,点B表示的为![]() ,C点位置在-2至3之间(包括边界点),若C点表示的数为
,C点位置在-2至3之间(包括边界点),若C点表示的数为![]() ,则
,则![]() +
+![]() +
+![]() 的最小值为 ,
的最小值为 ,![]() +
+![]() +
+![]() 的最大值为 .
的最大值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的边BC为直径的⊙O交AC于点D,过点D作⊙O的切线交AB于点E.
(1)如图1,若∠ABC=90°,求证:OE∥AC;
(2)如图2,已知AB=AC,若sin∠ADE=![]() , 求tanA的值.
, 求tanA的值.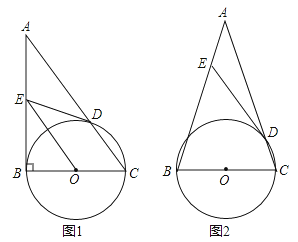
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A、B的距离,他们设计了如图所示的测量方案:从树A沿着垂直于AB的方向走到E,再从E沿着垂直于AE的方向走到F,C为AE上一点,其中3位同学分别测得三组数据:①AC,∠ACB;②EF、DE、AD;③CD,∠ACB,∠ADB.其中能根据所测数据求得A、B两树距离的有( )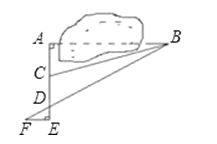
A.0组
B.一组
C.二组
D.三组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的“杨辉三角”告诉了我们二项式乘方展开式的系数规律.如:第三行的三个数(1,2,1)恰好对应着![]() 的展开式
的展开式![]() 的系数;第四行的四个数恰好对应着
的系数;第四行的四个数恰好对应着![]() 的展开式
的展开式![]() 的系数;根据数表中前五行的数字所反映的规律,回答:
的系数;根据数表中前五行的数字所反映的规律,回答:
(1)写出图中第六行括号里的数字;(请按从左到右的顺序填写)

(2)求![]() ;
;
(3)利用上面规律计算求值:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当n为1,2,3,…时,由大小相同的小正方形组成的图形如图所示,则第10个图形中小正方形的个数总和等于( )
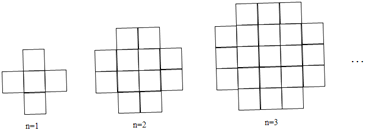
A. 100 B. 96 C. 144 D. 140
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com