
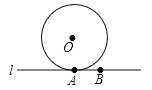
【题目】如图,已知⊙O的半径为5,直线l切⊙O于A,在直线l上取点B,AB=4.
(1)请用无刻度的直尺和圆规,过点B作直线m⊥l,交⊙O于C、D(点D在点C的上方);(保留作图痕迹,不要求写作法)
(2)求BC的长.
【答案】(1)答案见解析;(2)2.
【解析】试题分析:(1)利用基本作图(过一点作已知直线的垂线)作直线m得到CD;
(2)作OH⊥CD于H,连接OA、OD,如图,利用垂径定理得到DH=CH,则根据切线的性质得OA⊥l,易得四边形OABH为正方形,所以OH=AB=4,BH=OA=5,然后利用勾股定理计算出DH=3,则CH=3,所以BC=BH﹣CH=2.
试题解析:解:(1)如图,CD为所作;
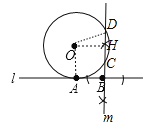
(2)作OH⊥CD于H,连接OA、OD,如图,则DH=CH.∵直线l切⊙O于A,∴OA⊥l,易得四边形OABH为正方形,∴OH=AB=4,BH=OA=5.在Rt△ODH中,DH=![]() =3,∴CH=3,∴BC=BH﹣CH=5﹣3=2.
=3,∴CH=3,∴BC=BH﹣CH=5﹣3=2.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c (a、b、c为常数且a≠0)中的x与y的部分对应值如下表,
x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 12 | 5 | 0 | -3 | -4 | -3 | 0 | 5 | 12 | … |
下列四个结论:
(1)二次函数y=ax2+bx+c 有最小值,最小值为-3;
(2)抛物线与y轴交点为(0,-3);
(3)二次函数y=ax2+bx+c 的图像对称轴是x=1;
(4)本题条件下,一元二次方程ax2+bx+c的解是x1=-1,x2=3.
其中正确结论的个数是( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
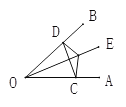
【题目】如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.
求证:(1)∠ECD=∠EDC;
(2)OC=OD;
(3)OE是线段CD的垂直平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BCD=110°,AB的垂直平分线交对角线AC于点F,E为垂足,连接DF,则∠CDF等于( )

A. 15° B. 25° C. 45° D. 55°
查看答案和解析>>
科目:初中数学 来源: 题型:
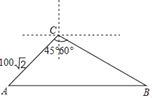
【题目】在某校组织的“交通安全宣传教育月”活动中,八年级数学兴趣小组的同学进行了如下的课外实践活动.具体内容如下:在一段笔直的公路上选取两点A、B,在公路另一侧的开阔地带选取一观测点C,在C处测得点A位于C点的南偏西45°方向,且距离为100![]() 米,又测得点B位于C点的南偏东60°方向.已知该路段为乡村公路,限速为60千米/时,兴趣小组在观察中测得一辆小轿车经过该路段用时13秒,请你帮助他们算一算,这辆小车是否超速?(参考数据:
米,又测得点B位于C点的南偏东60°方向.已知该路段为乡村公路,限速为60千米/时,兴趣小组在观察中测得一辆小轿车经过该路段用时13秒,请你帮助他们算一算,这辆小车是否超速?(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,计算结果保留两位小数)
≈1.73,计算结果保留两位小数)
查看答案和解析>>
科目:初中数学 来源: 题型:
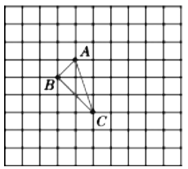
【题目】如图,正方形网格中的![]() ,若小方格边长为1,格点三角形(顶点是网格线的交点的三角形)
,若小方格边长为1,格点三角形(顶点是网格线的交点的三角形)![]() 的顶点
的顶点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() .
.
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)作出三角形![]() 关于y 轴对称的三角形
关于y 轴对称的三角形![]() ;
;
(3)判断![]() 的形状.
的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+2![]() =(1+
=(1+![]() )2,善于思考的小明进行了以下探索:设a+
)2,善于思考的小明进行了以下探索:设a+![]() b=(m+
b=(m+![]() n)2(其中a,b,m,n均为正整数),则有a+
n)2(其中a,b,m,n均为正整数),则有a+![]() b=m2+2n2+2
b=m2+2n2+2![]() mn,∴a=m2+2n2,b=2mn.这样小明就找到了一种把a+
mn,∴a=m2+2n2,b=2mn.这样小明就找到了一种把a+![]() b化为平方式的方法.
b化为平方式的方法.
请你仿照小明的方法探索并解决下列问题.
(1)当a、b、m、n均为正整数时,若a+![]() b=(m+
b=(m+![]() n)2,用含m、n的式子分别表示a、b,则a= ,b= ;
n)2,用含m、n的式子分别表示a、b,则a= ,b= ;
(2)求7+4![]() 的算术平方根.
的算术平方根.
查看答案和解析>>
科目:初中数学 来源: 题型:
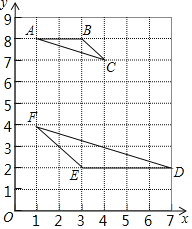
【题目】如图,在平面直角坐标系中,每个小方格都是边长为1个单位的小正方形,点A、B、C都是格点![]() 每个小方格的顶点叫格点
每个小方格的顶点叫格点![]() ,其中
,其中![]() ,
,![]() ,
,![]() .
.
![]() 外接圆的圆心坐标是______;
外接圆的圆心坐标是______;
![]() 外接圆的半径是______;
外接圆的半径是______;
![]() 已知
已知![]() 与
与![]() 点D、E、F都是格点
点D、E、F都是格点![]() 成位似图形,则位似中心M的坐标是______;
成位似图形,则位似中心M的坐标是______;
![]() 请在网格图中的空白处画一个格点
请在网格图中的空白处画一个格点![]() ,使
,使![]() ∽
∽![]() ,且相似比为
,且相似比为![]() :1.
:1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com