
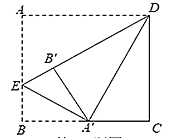
����Ŀ����ͼ1������ABC�У�AC��nAB����CAB��������E��F�ֱ���AB��AC����EF��BC������AEF�Ƶ�A˳ʱ����ת����ͼ2��λ�ã�����CF��BE��
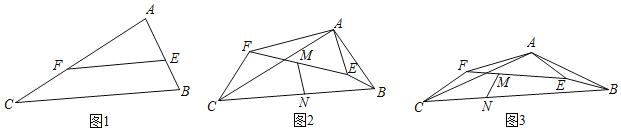
��1����֤����ACF����ABE��
��2������M��N�ֱ���EF��BC���е㣬������90��ʱ����֤��BE2+CF2��4MN2��
��3����ͼ3����M��N�ֱ���EF��BC����![]() ��
��![]() ��
��![]() ����n��
����n��![]() ������135����BE��
������135����BE��![]() ��ֱ��д��MN�ij���
��ֱ��д��MN�ij���
���𰸡���1������������2������������3��![]()
��������
��1��֤����CAF�ס�BAE���ɽ�����⣻
��2���ӳ�BE��CF���ӳ�����H������BF��ȡBF���е�J������NJ��JM����AC��BH�ڵ�O������֤��CF��BE�����������ε���λ�߶���֤����NJM��ֱ�������Σ����ù��ɶ������ɽ�����⣮
��3����ͼ3�У��ӳ�BE��CF���ӳ�����H������BF����FB��ȡһ��J��ʹ��FJ��JB��1��2������NJ��JM��֤����MJN��45����NJ��![]() ��MJ��
��MJ��![]() ����ͼ4�У�����NJM�У���MK��NJ��K����ֱ�����������MN���ɣ�
����ͼ4�У�����NJM�У���MK��NJ��K����ֱ�����������MN���ɣ�
��1��֤����

����ͼ1�У�
��EF��BC��
��![]() ��
��
��![]() ��
��
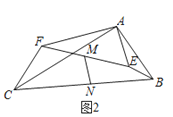
��ͼ2�У�
�ߡ�CAB����EAF��
���CAF����BAE��
��![]() ��
��
���CAF�ס�BAE��
���ACF����ABE��
��2��֤������ͼ2�У��ӳ�BE��CF���ӳ�����H������BF��ȡBF���е�J������NJ��JM����AC��BH�ڵ�O��
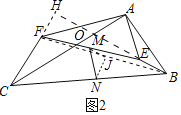
�ߡ�OCH����OBA����COH����BOA��
���H����OAB��90����
��CF��BE��
��CN��BN��FJ��JB��
��JN��CF��JN��![]() CF��
CF��
��FM��ME��FJ��JB��
��MJ��BE��MJ��![]() BE��
BE��
��CF��BE��
��NJ��JM��
���NJM��90����
��JN2+JM2��MN2��
�ࣨ![]() CF��2+��
CF��2+��![]() BE��2��MN2��
BE��2��MN2��
��BE2+CF2��4MN2��
��3���⣺��ͼ3�У��ӳ�BE��CF���ӳ�����H������BF����FB��ȡһ��J��ʹ��FJ��JB��1��2������NJ��JM��
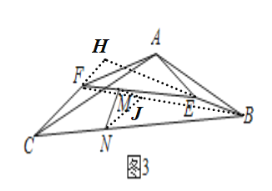
ͬ����֤��H����CAB��135����
��CN��BN��FJ��JB��1��2��
��NJ��CF��NJ��![]() CF��
CF��
��FM��ME��FJ��JB��1��2��
��MJ��BE��MJ��![]() BE��
BE��
���MJN�С�MJN�����Ϊ135����
���MJN��45����
������BE��![]() ��CF��2��
��CF��2��
��NJ��![]() ��MJ��
��MJ��![]() ��
��
��ͼ4�У�����NJM�У���MK��NJ��K��

�ߡ�J����JMK��45����MJ��![]() ��
��
��MK��KJ��![]() ��
��
��NK��NJ��KJ��1��
��MN��![]() =
=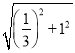 ��
��![]() ��
��


 ͬ����ϰǿ����չϵ�д�
ͬ����ϰǿ����չϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪ƽ���ı���![]() �У�
��![]() ��
��![]() ��
��![]() .ƽ���ı���
.ƽ���ı���![]() �Ķ���
�Ķ���![]() ���߶�
���߶�![]() �ϣ���
�ϣ���![]() ��
��![]() ����ߣ�������
����ߣ�������![]() �ֱ����߶�
�ֱ����߶�![]() ��
��![]() ��.
��.
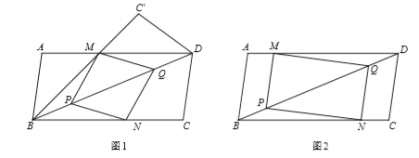
��1����֤��![]() ��
��
��2����ͼ1����![]() ��ֱ��
��ֱ��![]() �۵��õ�
�۵��õ�![]() ����
����![]() ǡ�þ�����
ǡ�þ�����![]() ʱ����֤���ı���
ʱ����֤���ı���![]() �����Σ�
������
��3����ͼ2�����ı���![]() �Ǿ��Σ���
�Ǿ��Σ���![]() ����
����![]() �ij�.������еķ�ĸ�ɱ�����ʽ��
�ij�.������еķ�ĸ�ɱ�����ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��C����B�ص������������д�ɽ�������B�ص�C��������A�أ���֪A��λ��B�ر�ƫ��53��������B��516ǧ�ף�C��λ��A����ƫ��45�������ִ����ͨ��ɽ��������������ֱ��������ɸ������B��ǰ��C�ص�·�̣��������ȷ��1ǧ�ף����ο����ݣ�sin53����![]() ��cos53����
��cos53����![]() ��tan53����
��tan53����![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
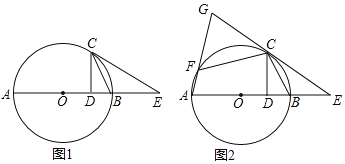
����Ŀ����ͼ1��ABΪ��O��ֱ����CΪ��O��һ�㣬����CB����C��CD��AB�ڵ�D������C����BCE��ʹ��BCE����BCD������CE��AB���ӳ����ڵ�E��
��1����֤��CE����O�����ߣ�
��2����ͼ2����F����O�ϣ��������FCE��2��ABC������AF���ӳ���EC���ӳ����ڵ�G��
����̽���߶�CF��CD֮�������������ϵ��
����CD��4��BD��2�����߶�FG�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB����O��ֱ����C����0�ϵ�һ�㣬ֱ��MN������C������A��ֱ��MN�Ĵ��ߣ�����Ϊ��D������BAC=��DAC

��1������ֱ��MN����O��λ�ù�ϵ����˵�����ɣ�
��2����CD=6��cos��ACD=![]() ������O�İ뾶��
������O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У��Խ���AC��BD�ཻ�ڵ�O��EΪOC�϶���(���O���غ�)����AF��BE������ΪG����BC��F����B0��H������OG��CC��
(1)��֤��AH=BE��
(2)��̽������AGO�Ķ����Ƿ�Ϊ��ֵ?��˵�����ɣ�
(3)��OG��CG��BG=![]() ������OGC�������
������OGC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪AB�ǡ�O��ֱ������CD��AB��H����CD�ӳ�����һ��E����O�����߽�AB���ӳ�����F���е�ΪG������AG��CD��K��
��1����ͼ1����֤��KE=GE��
��2����ͼ2������CABG������FGB=![]() ��ACH����֤��CA��FE��
��ACH����֤��CA��FE��
��3����ͼ3���ڣ�2���������£�����CG��AB�ڵ�N����sinE=![]() ��AK=
��AK=![]() ����CN�ij���
����CN�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AB��CD��2AB=2BC=CD=10��tanB=![]() ����AD=______��
����AD=______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���![]() �У�
��![]() ����
����![]() ���ڷ��ۣ���
���ڷ��ۣ��� ![]() ����
����![]() �ϣ���Ϊ
�ϣ���Ϊ![]() ���ۺ�Ϊ
���ۺ�Ϊ![]() ������
������![]() ��
��![]() ���ڷ��ۣ���
���ڷ��ۣ���![]() ǡ�� ����
ǡ�� ����![]() �ϣ���Ϊ
�ϣ���Ϊ![]() ����
����![]() �ij��� ��
�ij��� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com