
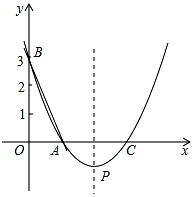
 ��ͼ��ֱ��y=-3x+3��x�ᡢy��ֱ��ڵ�A��B��������y=a��x-2��2+k������A��B������X�ύ����һ��C���䶥��ΪP��
��ͼ��ֱ��y=-3x+3��x�ᡢy��ֱ��ڵ�A��B��������y=a��x-2��2+k������A��B������X�ύ����һ��C���䶥��ΪP������ ��1�������ֱ��y=-3x+3��x�ύ��A����y�ύ��B�����꣬�ٽ�A��B�����������y=a��x-2��2+k���õ�����a��k�Ķ�Ԫһ�η����飬�ⷽ���鼴����⣻
��2����Q�������Ϊ��2��m�����Գ���x=2��x���ڵ�F������B��BE��ֱ��ֱ��x=2�ڵ�E����Rt��AQF��Rt��BQE�У��ù��ɶ����ֱ��ʾ��AQ2=AF2+QF2=1+m2��BQ2=BE2+EQ2=4+��3-m��2����AQ=BQ���õ�����1+m2=4+��3-m��2���ⷽ�����m=2���������Q������ꣻ
��3������N�ڶԳ�����ʱ����NC��AC����ֱ���ó�ACΪ�����εĶԽ��ߣ����������ߵĶԳ��Լ������ε����ʣ��õ�M���붥��P��2��-1���غϣ�N��Ϊ��P����x��ĶԳƵ㣬��ʱ��MF=NF=AF=CF=1����AC��MN�����ı���AMCNΪ�����Σ���Rt��AFN�и��ݹ��ɶ���������������εı߳���
��� �⣺��1����ֱ��y=-3x+3��x�ᡢy��ֱ��ڵ�A��B��
��A��1��0����B��0��3����
�֡�������y=a��x-2��2+k������A��1��0����B��0��3����
��$\left\{\begin{array}{l}{a+k=0}\\{4a+k=3}\end{array}\right.$�����$\left\{\begin{array}{l}{a=1}\\{k=-1}\end{array}\right.$��
��a��k��ֵ�ֱ�Ϊ1��-1��
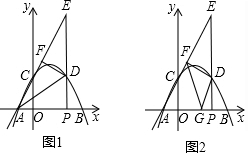
��2����ͼ1��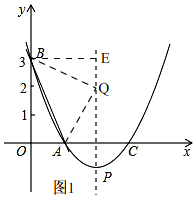
��Q�������Ϊ��2��m�����Գ���x=2��x���ڵ�F������B��BE��ֱ��ֱ��x=2�ڵ�E��
��Rt��AQF��AQ2=AF2+QF2=1+m2��
��Rt��BQE��BQ2=BE2+EQ2=4+��3-m��2��
��AQ=BQ��
��1+m2=4+��3-m��2��
��m=2��
��Q���������2��2����
��3����ͼ2��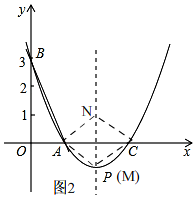
����N�ڶԳ�����ʱ��NC��AC����ֱ������ACӦΪ�����εĶԽ��ߣ�
�߶Գ���x=2��AC���д��ߣ�
��M���붥��P��2��-1���غϣ�N��Ϊ��P����x��ĶԳƵ㣬������Ϊ��2��1����
��ʱ��MF=NF=AF=CF=1����AC��MN��
���ı���AMCNΪ�����Σ�
��Rt��AFN��AN=$\sqrt{A{F}^{2}+N{F}^{2}}$=$\sqrt{2}$��
�������εı߳�Ϊ$\sqrt{2}$��
���� �����Ƕ��κ������ۺ��⣬��Ҫ�����˶�Ԫһ�η�����Ľⷨ�����������ε����ʣ����ɶ��������κ��������ʣ������ε��ж������ʣ��ۺ��Խ�ǿ���Ѷ����У����Ȿ��Ĺؼ����ù��ɶ��������Q�����꣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �� | B�� | �Ǹ��� | C�� | ���� | D�� | ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
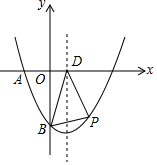 ��ͼ����ƽ��ֱ������ϵ�У����κ���y=ax2-$\frac{3}{2}$x+c��a��0����ͼ����x�ύ��A��-2��0����C���㣬��y�ύ�ڵ�B��0��-4������Գ�����x�ύ�ڵ�D��
��ͼ����ƽ��ֱ������ϵ�У����κ���y=ax2-$\frac{3}{2}$x+c��a��0����ͼ����x�ύ��A��-2��0����C���㣬��y�ύ�ڵ�B��0��-4������Գ�����x�ύ�ڵ�D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ1����֪������y=-$\frac{1}{3}$x2+$\frac{1}{3}$x+4��x�ύ��A��B���㣨B����A���ұߣ�����y�ύ��C�㣬PΪ�߶�OB��һ���㣬��P��x�ᴹ�߽���������D�㣬��ֱ��AC��E�㣬��D����DF��AE������ΪF����P��ĺ�����Ϊm��
��ͼ1����֪������y=-$\frac{1}{3}$x2+$\frac{1}{3}$x+4��x�ύ��A��B���㣨B����A���ұߣ�����y�ύ��C�㣬PΪ�߶�OB��һ���㣬��P��x�ᴹ�߽���������D�㣬��ֱ��AC��E�㣬��D����DF��AE������ΪF����P��ĺ�����Ϊm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | -1 | C�� | -1��1 | D�� | ���������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com