
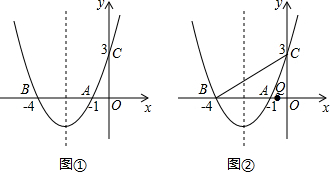
���� ��1������A��B��C��������꣬���ô���ϵ��������������߽���ʽ��
��2��A��B������ڶԳ���Գƣ�����BC���Գ����ڵ�P����P�㼴Ϊ������Rt��BOC�п����BC�ij�����һ��������ı���PAOC�ܳ�����Сֵ��
��3���֡�MQB=90��͡�QMB=90��������������M�����꣬�ٸ��ݡ�CQMΪ���������Σ�������������ƿɵõ�����M������ķ��̣������M�����꣮
��� �⣺
��1���������߽���ʽΪy=ax2+bx+c��a��0����
�������֪A��-1��0����B��-4��0����C��0��3����
���������߽���ʽ�ɵ�$\left\{\begin{array}{l}{a-b+c=0}\\{16a-4b+c=0}\\{c=3}\end{array}\right.$�����$\left\{\begin{array}{l}{a=\frac{3}{4}}\\{b=\frac{15}{4}}\\{c=3}\end{array}\right.$��
�������߽���ʽΪy=$\frac{3}{4}$x2+$\frac{15}{4}$x+3��
��2����A��B���ڶԳ���Գƣ���ͼ1������BC��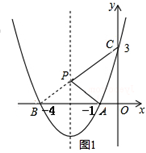
��BC��Գ���Ľ��㼴Ϊ����ĵ�P����ʱPA+PC=BC��
���ı���PAOC���ܳ���СֵΪ��OC+OA+BC��
��A��-1��0����B��-4��0����C��0��3����
��OA=1��OC=3��BC=$\sqrt{O{B}^{2}+O{C}^{2}}$=5��
��OC+AB+BC=1+3+5=9��
���������ߵĶԳ����ϴ��ڵ�P��ʹ�ı���PAOC���ܳ���С���ı���PAOC�ܳ�����СֵΪ9��
��3����ֱ��BC����ʽΪy=kx+n��
��B��C�����������ɵ�$\left\{\begin{array}{l}{-4k+n=0}\\{n=3}\end{array}\right.$�����$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{n=3}\end{array}\right.$��
��ֱ��BC�Ľ���ʽΪy=$\frac{3}{4}$x+3��
�ٵ���BQM=90��ʱ����ͼ2����M��a��b����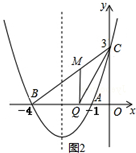
�ߡ�CMQ��90�㣬
��ֻ��CM=MQ=b��
��MQ��y�ᣬ
���MQB�ס�COB��
��$\frac{BM}{BC}$=$\frac{MQ}{OC}$����$\frac{5-b}{5}$=$\frac{b}{3}$��
���b=$\frac{15}{8}$������y=$\frac{3}{4}$x+3�ɵ�$\frac{15}{8}$=$\frac{3}{4}$a+3��
���a=-$\frac{3}{2}$��
��M��������-$\frac{3}{2}$��$\frac{15}{8}$����
�ڵ���QMB=90��ʱ����ͼ3��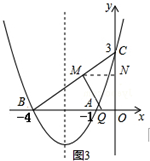
�ߡ�CMQ=90�㣬
��ֻ��CM=MQ��
��CM=MQ=m����BM=5-m��
�ߡ�BMQ=��COB=90�㣬��MBQ=��OBC��
���BMQ�ס�BOC��
��$\frac{5-m}{4}$=$\frac{m}{3}$�����m=$\frac{15}{7}$��
��MN��OB������$\frac{MN}{OB}$=$\frac{CN}{OC}$=$\frac{CM}{BC}$��
��$\frac{MN}{4}$=$\frac{CN}{3}$=$\frac{\frac{15}{7}}{5}$��
��MN=$\frac{12}{7}$��CN=$\frac{9}{7}$��
��ON=OC-CN=3-$\frac{9}{7}$=$\frac{12}{7}$��
��M��������-$\frac{12}{7}$��$\frac{12}{7}$����
���Ͽ�֪���߶�BC���Ǵ��������ĵ�M��ʹ��CQMΪ�����������ҡ�BQMΪֱ�������Σ���M������Ϊ
��-$\frac{3}{2}$��$\frac{15}{8}$����-$\frac{12}{7}$��$\frac{12}{7}$����
���� ����Ϊ���κ������ۺ�Ӧ�ã��漰֪ʶ���д���ϵ��������ԳƵ����ʺ�Ӧ�á����������ε����ʡ����������ε��ж������ʼ���������˼�룮�ڣ�2����ȷ����P���λ���ǽ���Ĺؼ����ڣ�3����ע�������������������ۣ����õ��������ε����ʵõ������ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���Ѷ����У�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��A=��C | B�� | �Խ���AC��BD����ƽ�� | ||
| C�� | AB=CD | D�� | �Խ���AC��BD���ഹֱ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
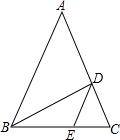 ��ͼ���ڡ�ABC�У�AB=AC����A=36�㣬BDƽ�֡�ABC��AC�ڵ�D������D��DE��AB����BC�ڵ�E�����н����д�����ǣ�������
��ͼ���ڡ�ABC�У�AB=AC����A=36�㣬BDƽ�֡�ABC��AC�ڵ�D������D��DE��AB����BC�ڵ�E�����н����д�����ǣ�������| A�� | DEƽ�֡�BDC | B�� | ��ABC�ס�BDC�ס�DEC | C�� | $\frac{AD}{AB}$=$\frac{\sqrt{5}-1}{2}$ | D�� | $\frac{{S}_{��BCD}}{{S}_{��ABD}}$=$\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| 1�� | 2�� | 3�� | 4�� | 5�� | ƽ������ | ���� | |
| �װ� | 150 | 148 | 160 | 139 | 153 | 150 | 46.8 |
| �Ұ� | 139 | 150 | 145 | 169 | 147 | a | 103.2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABC�ա�CDA��AD��BC���ڵ�P����BCA=40�㣬���APB=80���ȣ���
��ͼ����ABC�ա�CDA��AD��BC���ڵ�P����BCA=40�㣬���APB=80���ȣ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����ƽ��ֱ������ϵ�У��� B�������ǣ�-2��0������A��y���������ϵ�һ�㣬�ҡ�BAO=30�㣬�ֽ���BAO˳ʱ����ת90������DCO��ֱ��l���߶�BC�Ĵ�ֱƽ���ߣ���P��l��һ���㣬��PA+PB����СֵΪ��������
��ͼ����ƽ��ֱ������ϵ�У��� B�������ǣ�-2��0������A��y���������ϵ�һ�㣬�ҡ�BAO=30�㣬�ֽ���BAO˳ʱ����ת90������DCO��ֱ��l���߶�BC�Ĵ�ֱƽ���ߣ���P��l��һ���㣬��PA+PB����СֵΪ��������| A�� | 2$\sqrt{6}$ | B�� | 4 | C�� | 2$\sqrt{3}$+1 | D�� | 2$\sqrt{3}$+2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com