
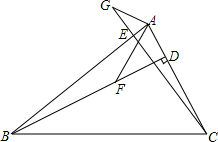
 已知:BD,CE是△ABC的高,点F在BD上,BF=AC,点G在CE的延长线上,CG=AB.
已知:BD,CE是△ABC的高,点F在BD上,BF=AC,点G在CE的延长线上,CG=AB.
|


科目:初中数学 来源: 题型:
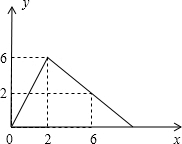 某医药研究所开发了一种新药,在实验药效时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(微克)随时间x(时)的变化情况如图所示,当成人按规定服药后:
某医药研究所开发了一种新药,在实验药效时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(微克)随时间x(时)的变化情况如图所示,当成人按规定服药后:查看答案和解析>>
科目:初中数学 来源: 题型:
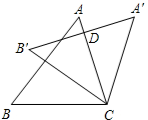 如图,将三角形△ABC绕着点C顺时针旋转35°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=90°,则∠A的度数是( )
如图,将三角形△ABC绕着点C顺时针旋转35°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=90°,则∠A的度数是( )| A、35° | B、65° |
| C、55° | D、25° |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、350 | B、595 |
| C、666 | D、406 |
查看答案和解析>>
科目:初中数学 来源: 题型:
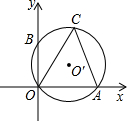 如图,CO、CA是⊙O′的弦,⊙O′与坐标系x、y轴分别交于点A、B,B点坐标为(0,2),∠ACO=60°,则⊙O′的直径为( )
如图,CO、CA是⊙O′的弦,⊙O′与坐标系x、y轴分别交于点A、B,B点坐标为(0,2),∠ACO=60°,则⊙O′的直径为( )| A、2 | ||
B、
| ||
| C、4 | ||
| D、5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com