
分析 (1)设大车用x辆,小车用y辆.依据题意,得:x+y=20,15x+10y=240求出即可,
(2)根据题意得出总运费w=630x+420(10-x)+750×(8-x)+550(10-8+x)=10x+11300,由解析式可知当x取最小值时,w最小,然后根据运往A地的白砂糖不少于115吨列出不等式求得x的最小值,求出即可.
解答 解:(1)设大货车x辆,小货车y辆,则$\left\{\begin{array}{l}{x+y=20}\\{15x+10y=240}\end{array}\right.$,
解方程组,得 $\left\{\begin{array}{l}{x=8}\\{y=12}\end{array}\right.$,
答:两种货车分别为8和12辆;
(2)设安排x辆大货车前往A地,则(10-x)辆小货车前往A地,(8-x)辆大货车前往B地,(12-10+x)辆小货车前往B地,
总运费:w=630x+420(10-x)+750×(8-x)+550(12-10+x)=10x+11300;
因为15x+10(10-x)≥115,则x≥3,
所以当x=3时,w最小,
w最小=10×3+11300=11330(元)
答:最少总运费为11330元.
点评 此题主要考查了二元一次方程组的应用和一元一次不等式的应用,根据已知得出等式方程和不等式进而求出是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
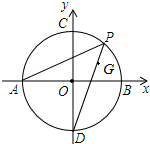 如图,在平面直角坐标系中,半径为4的⊙O交坐标轴于A、B、C、D,点P为 弧BC上一个点(不与B、C点重合),连结PD.若△PAB的内切圆圆心为G,半径为1,则PD=5$\sqrt{2}$.
如图,在平面直角坐标系中,半径为4的⊙O交坐标轴于A、B、C、D,点P为 弧BC上一个点(不与B、C点重合),连结PD.若△PAB的内切圆圆心为G,半径为1,则PD=5$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -(2x+y)=-2x+y | B. | 2(x-y)=2x-y | C. | 3x-(2y+z)=3x-2y-z | D. | x-(-y+z)=x-y-z |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com