
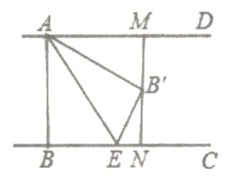
【题目】如图,已知![]() ,点
,点![]() 为射线
为射线![]() 上一个动点,连接
上一个动点,连接![]() ,将
,将![]() 沿
沿![]() 折叠,点
折叠,点![]() 落在点
落在点![]() 处,过点
处,过点![]() 作
作![]() 的垂线,分别交
的垂线,分别交![]() 于点
于点![]() 当点
当点![]() 为线段
为线段![]() 的三等分点时,
的三等分点时,![]() 的长为_____________
的长为_____________
科目:初中数学 来源: 题型:
【题目】如图所示,平面直角坐标系xOy中,矩形ABCD的边AB=4,BC=6.在不改变矩形ABCD的形状和大小的情况下,当矩形的顶点A在x轴的正半轴上左右移动时,另一个顶点D始终在y轴的正半轴上随之上下移动.
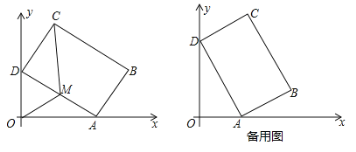
(1)当∠OAD=30°时,求点C的坐标;
(2)设AD的中点为M,连接OM、MC,若四边形OMCD的面积为![]() 时,求OA的长;
时,求OA的长;
(3)在点A移动过程中是否存在某一位置,使点C到点O的距离有最大值?若存在,求此时的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自我省深化课程改革以来,某校开设了:A.利用影长求物体高度,B.制作视力表,C.设计遮阳棚,D.制作中心对称图形,四类数学实践活动课.规定每名学生必选且只能选修一类实践活动课,学校对学生选修实践活动课的情况进行抽样调查,将调查结果绘制成如下两幅不完整的统计图.
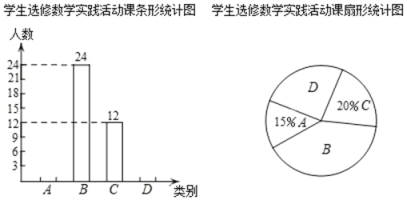
根据图中信息解决下列问题:
(1)本次共调查名学生,扇形统计图中B所对应的扇形的圆心角为度;
(2)补全条形统计图;
(3)选修D类数学实践活动的学生中有2名女生和2名男生表现出色,现从4人中随机抽取2人做校报设计,请用列表或画树状图法求所抽取的两人恰好是1名女生和1名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() ,
,![]() ,
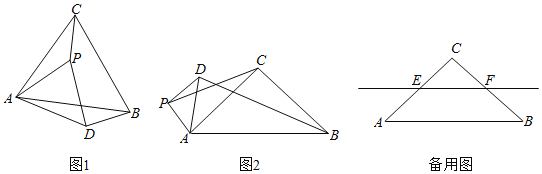
,![]() .点P是平面内不与点A,C重合的任意一点.连接AP,将线段AP绕点P逆时针旋转α得到线段DP,连接AD,BD,CP.
.点P是平面内不与点A,C重合的任意一点.连接AP,将线段AP绕点P逆时针旋转α得到线段DP,连接AD,BD,CP.
(1)观察猜想
如图1,当![]() 时,
时,![]() 的值是 ,直线BD与直线CP相交所成的较小角的度数是 .
的值是 ,直线BD与直线CP相交所成的较小角的度数是 .
(2)类比探究
如图2,当![]() 时,请写出
时,请写出![]() 的值及直线BD与直线CP相交所成的小角的度数,并就图2的情形说明理由.
的值及直线BD与直线CP相交所成的小角的度数,并就图2的情形说明理由.
(3)解决问题
当![]() 时,若点E,F分别是CA,CB的中点,点P在直线EF上,请直接写出点C,P,D在同一直线上时
时,若点E,F分别是CA,CB的中点,点P在直线EF上,请直接写出点C,P,D在同一直线上时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乡镇实施产业扶贫,帮助贫困户承包了荒山种植某品种蜜柚.到了收获季节,已知该蜜柚的成本价为![]() ,投人市场销售时,调査市场行情,发现该蜜柚销售不会亏本,且每天销售量
,投人市场销售时,调査市场行情,发现该蜜柚销售不会亏本,且每天销售量![]() (单位:千克)与销售单价
(单位:千克)与销售单价![]() (单位:
(单位: ![]() )之间的函数关系如图
)之间的函数关系如图
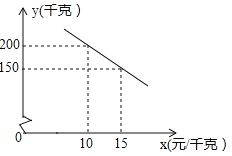
(1)求![]() 与
与![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围;
的取值范围;
(2)当该品种蜜柚定价为多少时,每天销售获得的利润最大,最大利润是多少?
(3)某农户今年共采摘蜜柚4800千克,该品种蜜柚的保质期为40天,根据(2)中获得最大利润的方式进行销售,能否销售完这批蜜柚?请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 中,点
中,点![]() 是
是![]() 边的中点.将
边的中点.将![]() 沿
沿![]() 对折至
对折至![]() ,延长
,延长![]() 交
交![]() 边于点
边于点![]() ,连接
,连接![]() ,
,![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的有( )
.其中正确的有( )
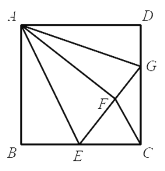
A.①②B.①③④C.②③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小花在一次放风筝活动中某时段的示意图,她在A处时的风筝线(整个过程中风筝线近似地看作直线)与水平线构成30°角,线段AA1表示小花身高1.5米,当她从点A跑动9![]() 米到达点B处时,风筝线与水平线构成45°角,此时风筝到达点E处,风筝的水平移动距离CF=10
米到达点B处时,风筝线与水平线构成45°角,此时风筝到达点E处,风筝的水平移动距离CF=10![]() 米,这一过程中风筝线的长度保持不变,求风筝原来的高度C1D.
米,这一过程中风筝线的长度保持不变,求风筝原来的高度C1D.

查看答案和解析>>
科目:初中数学 来源: 题型:
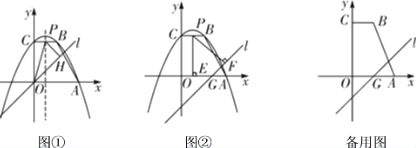
【题目】(2018郑州模拟)如图,抛物线![]() 过点
过点![]() ,与y轴交于点C.
,与y轴交于点C.
(1)求该抛物线的解析式;
(2)如图①,直线l的解析式为![]() ,抛物线的对称轴与线段BC交于点P,过点P作直线l的垂线,垂足为点H,连接OP,求
,抛物线的对称轴与线段BC交于点P,过点P作直线l的垂线,垂足为点H,连接OP,求![]() 的面积;
的面积;
(3)把图①中的直线![]() 向下平移4个单位长度得到直线
向下平移4个单位长度得到直线![]() ,如图②,直线
,如图②,直线![]() 与x轴交于点G.点P是四边形ABCO边上的一点,过点P分别作x轴、直线l的垂线,垂足分别为点E、F.是否存在点P,使得以P、E、F为顶点的三角形是等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
与x轴交于点G.点P是四边形ABCO边上的一点,过点P分别作x轴、直线l的垂线,垂足分别为点E、F.是否存在点P,使得以P、E、F为顶点的三角形是等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】车间有20名工人,某天他们生产的零件个数统计如下表.
车间20名工人某一天生产的零件个数统计表
生产零件的个数(个) | 9 | 10 | 11 | 12 | 13 | 15 | 16 | 19 | 20 |
工人人数(人) | 1 | 1 | 6 | 4 | 2 | 2 | 2 | 1 | 1 |
(1)求这一天20名工人生产零件的平均个数;
(2)为了提高大多数工人的积极性,管理者准备实行“每天定额生产,超产有奖”的措施.如果你是管理者,从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com