
分析 过E点作MN⊥AD,利用AAS证明△DME与△CNE全等,再利用梯形的面积公式进行解答即可.
解答 解:过E点作MN⊥AD,如图: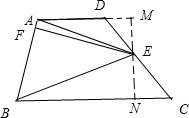 ,
,
在△DME与△CNE中,
$\left\{\begin{array}{l}{∠DME=∠CNE=90°}\\{∠NEC=∠MED}\\{DE=EC}\end{array}\right.$,
∴△DME≌△CNE(AAS),
∴ME=EN,
∵${S}_{梯形ABCD}=\frac{1}{2}(AD+BC)×(ME+EN)=(AD+BC)×ME$,
∵${S}_{梯形ABCD}={S}_{△ADE}+{S}_{△BEC}+{S}_{△ABE}=\frac{1}{2}AD×ME+\frac{1}{2}BC×ME+\frac{1}{2}×AB×EF$,
∴$\frac{1}{2}(AD+BC)×ME=\frac{1}{2}×AB×EF=\frac{1}{2}×5×3=7.5$,
∴四边形ABCD的面积为15cm2,
故答案为:15
点评 此题考查全等三角形的判定和性质,关键是过E点作MN⊥AD,利用AAS证明△DME与△CNE全等.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
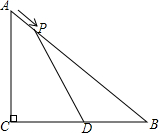 如图,在△ABC中,∠ACB=90°,AC=3cm,BC=4cm,点D为BC的中点.动点P从点A出发,沿着A→B方向以1cm/s的速度运动到点B停止运动.点P移动的时间为t秒,当△DBP为等腰三角形,求出t的值.
如图,在△ABC中,∠ACB=90°,AC=3cm,BC=4cm,点D为BC的中点.动点P从点A出发,沿着A→B方向以1cm/s的速度运动到点B停止运动.点P移动的时间为t秒,当△DBP为等腰三角形,求出t的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月使用费 单位:元 | 主叫限制时间 单位:分 | 主叫超时费 单位:分 | 被叫 | |
| 方式一 | 30 | 150 | 0.25 | 免费 |
| 方式二 | 50 | 350 | 0.16 | 免费 |
| t≤150 | 150<t<350 | t=350 | t>350 | |
| 方式一 计费/元 | 30 | 0.25t-7.5 | 80 | 0.25t-7.5 |
| 方式二 计费/元 | 50 | 50 | 50 | 0.16t-6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com