练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．为庆祝中国共产党建党90周年，某校举行了合唱比赛．小明计算出了甲、乙两个合唱队队员身高的方差，S甲2=1.5，S乙2=2.5．则甲、乙两个合唱队队员的身高比较整齐的是（　　）
    A．甲乙一样B．甲C．乙D．无法确定

    分析 利用方差越大，则平均值的离散程度越大，稳定性也越小；反之，则它与其平均值的离散程度越小，稳定性越好，进而分析得出答案．

    解答 解：∵S甲2=1.5，S乙2=2.5，
    ∴S甲2＜S乙2，即甲合唱队队员的身高比较整齐，
    故选：B．

    点评 此题主要考查了方差的意义，正确理解方差的意义是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    8．求两个正整数的最大公约数是常见的数学问题，中国古代数学专著《九章算术》中便记载了求两个正整数最大公约数的一种方法--更相减损术，术曰：“可半者半之，不可半者，副置分母、子之数，以少成多，更相减损，求其等也．以等数约之”，意思是说，要求两个正整数的最大公约数，先用较大的数减去较小的数，得到差，然后用减数与差中的较大数减去较小数，以此类推，当减数与差相等时，此时的差（或减数）即为这两个正整数的最大公约数．
    例如：求91与56的最大公约数
    解：
    91-56=35
    56-35=21
    35-21=14
    21-14=7
    14-7=7
    所以91与56的最大公约数是7．
    请用以上方法解决下列问题：
    （1）求216与135的最大公约数；
    （2）求三个数156，52，143的最大公约数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

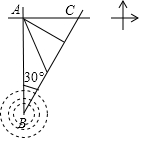    9．台风是一种自然灾害，它以台风中心为圆心，在周围数十千米范围内形气旋风暴，有极强的破坏力，此时某台风中心在海域B处，在沿海城市A的正南方向240千米，其中心风力为12级，每远离台风中心25千米，台风就会减弱一级，如图所示，该台风中心正以20千米/时的速度沿北偏东30°方向向C移动，且台风中心的风力不变，若城市所受风力达到或超过4级，则称受台风影响．
    试问：
    （1）A城市是否会受到台风影响？请说明理由．
    （2）若会受到台风影响，那么台风影响该城市的持续时间有多长？
    （3）该城市受到台风影响的最大风力为几级？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．（1）一个两位数的十位数字和个位数字之和是7，如果这个两位数加上45，则恰好成为个位数字与十位数字对调之后组成的两位数．求这个两位数．
    （2）加工某种工件，甲单独作要20天完成，乙只要10就能完成任务，现在要求二人在12天内完成任务．问乙需工作几天后甲再继续加工才可正好按期完成任务？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．已知两圆相交，它们的圆心距为3，一个圆的半径是2，那么另一个圆的半径长可以是（　　）
    A．1B．3C．5D．7

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．若平行四边形的一边长为5，它的两条对角线的长可能是（　　）
    A．4和3B．4和8C．4和6D．2和12

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．新定义：我们把两个面积相等但不全等的三角形叫做偏等积三角形．
    （1）初步尝试
    如图1，已知等腰直角△ABC，∠ACB=90°，请将它分成两个三角形，使它们成为偏等积三角形．
    （2）理解运用
    如图2，已知△ACD为直角三角形，∠ADC=90°，以AC，AD为边向外作正方向ACFB和正方形ADGE，连结BE，求证：△ACD与△ABE为偏等积三角形．
    （3）综合探究
    如图3，二次函数y=$\frac{1}{2}$x2-$\frac{3}{2}$x-5的图象与x轴交于A，B两点，与y轴交于点C，在二次函数的图象上是否存在一点D，使△ABC与△ABD是偏等积三角形？若存在，请求出点D的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

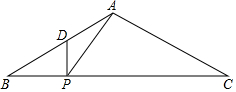    7．如图，在△ABC中，AB=AC=6，∠BAC=120°，点D是AB边上的点，$\frac{AD}{DB}$=$\frac{1}{2}$，点P为底边BC上的一动点，则△PDA周长的最小值为2$\sqrt{7}$+2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．如图，已知△ABC中，∠C=90°，BC=3，AC=4，BD平分∠ABC，将△ABC绕着点A旋转后，点B、C的对应点分别记为B1、C1，如果点B1落在射线BD上，那么CC1的长度为$\frac{16\sqrt{5}}{5}$．

    查看答案和解析>>

    同步练习册答案