
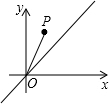
 如图,在平面直角坐标系中,点P的坐标为(1,2),将线段OP沿y轴正方向移动m(m>0)个单位长度至O′P′,以O′P′为直角边在第一象限内作等腰直角△O′P′Q,若点Q在直线y=x上,则m的值为2或3.
如图,在平面直角坐标系中,点P的坐标为(1,2),将线段OP沿y轴正方向移动m(m>0)个单位长度至O′P′,以O′P′为直角边在第一象限内作等腰直角△O′P′Q,若点Q在直线y=x上,则m的值为2或3. 分析 以O′P′为直角边在第一象限内作等腰直角△O′P′Q,需要分两种情况进行讨论,先根据等腰直角三角形的性质,判定全等三角形,再根据全等三角形的性质,得出对应边相等,最后根据线段的和差关系以及平移的方向,得出平移的距离即可.
解答  解:①如图所示,当△O′P′Q为等腰直角三角形时,过点P'作P'A⊥y轴于A,过Q作QB⊥y轴于B,则
解:①如图所示,当△O′P′Q为等腰直角三角形时,过点P'作P'A⊥y轴于A,过Q作QB⊥y轴于B,则
∠O'AP'=90°=∠QBO',∠P'O'Q=90°,
∴∠AO'P'+∠BO'Q=90°=∠O'QB+∠BO'Q,
∴∠AO'P'=∠O'QB,
又∵O'P'=QO',
∴△O'AP'≌△QBO',
∴AP'=BO',AO'=BQ,
∵点P的坐标为(1,2),
∴由平移可得,AP'=1,AO'=2,
∴BO'=1,
当点Q在直线y=x上时,BQ=2=BO,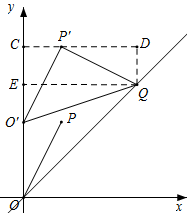
此时OO'=BO'+BO=1+2=3,
即平移的距离m为3;
②如图所示,过点P'作x轴的平行线交y轴于C,过点Q作y轴的平行线,交直线CP'于点D,
过点Q作QE⊥y轴于E,
同理可得,△O'CP'≌△P'DQ,
∴CE=DQ=CP'=1,DP'=CO'=2,
∴CD=EQ=1+2=3=OE,EO'=CO'-CE=2-1=1,
∴OO'=OE-O'E=3-1=2,
即平移的距离m为2,
故答案为:2或3.
点评 本题主要考查了全等三角形的判定与性质,等腰直角三角形的性质以及平移的性质,解决问题的关键是根据图形进行分类讨论,运用全等三角形的对应边相等进行计算求解.


 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:选择题
 如图,经过点B(1,0)的直线y=kx+b与直线y=4x+4相交于点A(m,$\frac{8}{3}$),则0<kx+b<4x+4的解集为( )
如图,经过点B(1,0)的直线y=kx+b与直线y=4x+4相交于点A(m,$\frac{8}{3}$),则0<kx+b<4x+4的解集为( )| A. | x<$\frac{1}{3}$ | B. | -$\frac{1}{3}$<x<1 | C. | x<1 | D. | -1<x<1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | $-3\sqrt{2}$ | D. | $3\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | p(1+10%)万元 | B. | (p+10%)万元 | C. | $\frac{p}{1+10%}$万元 | D. | $\frac{p}{1-10%}$万元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com