
分析 求代数式$\sqrt{{x^2}+4}+\sqrt{{{(12-x)}^2}+9}$的最小值.可以转化为在x轴上求一点P(x,0),使得点P到点A(0,2),点B(12,3)的距离之和最小.如图,作点A关于x轴的对称点A′,连接BA′由x轴的交点即为点P,作BM⊥y轴于M,利用勾股定理即可解决问题.
解答 解:求代数式$\sqrt{{x^2}+4}+\sqrt{{{(12-x)}^2}+9}$的最小值.可以转化为在x轴上求一点P(x,0),使得点P到点A(0,2),点B(12,3)的距离之和最小.
如图,作点A关于x轴的对称点A′,连接BA′由x轴的交点即为点P,作BM⊥y轴于M,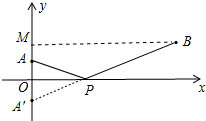
因为PA+PB的最小值=BA′=$\sqrt{A′{M}^{2}+B{M}^{2}}$=$\sqrt{{5}^{2}+1{2}^{2}}$=13.
所以代数式$\sqrt{{x^2}+4}+\sqrt{{{(12-x)}^2}+9}$的最小值为13.
点评 本题考查轴对称-最短问题、勾股定理等知识,解题的关键是学会转化的思想,把代数问题转化为几何问题,是数形结合的好题目,所以中考常考题型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
| x(人) | 500 | 1000 | 1500 | 2000 | 2500 | 3000 | … |
| y(元) | -3000 | -2000 | -1000 | 0 | 1000 | 2000 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 我们已经学过用面积来说明公式,如(x+y)2=x2+2xy+y2就可以用如图甲中的面积来说明,请写出图乙的面积所说明的公式:(p+x)(q+x)=x2+(p+q)x+pq.
我们已经学过用面积来说明公式,如(x+y)2=x2+2xy+y2就可以用如图甲中的面积来说明,请写出图乙的面积所说明的公式:(p+x)(q+x)=x2+(p+q)x+pq.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在如图的坐标平面上,有一条通过点(-3,-2)的直线l,若四点(-2,a)、(0,b)、(c,0)、(d,-1)在l上,则下列判断正确的是( )
在如图的坐标平面上,有一条通过点(-3,-2)的直线l,若四点(-2,a)、(0,b)、(c,0)、(d,-1)在l上,则下列判断正确的是( )| A. | a=3 | B. | b>-2 | C. | c<-3 | D. | d=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com