
【题目】如图,正方形ABCD的对角线交于点O,以AD为边向外作Rt△ADE,∠AED=90°,连接OE,DE=6,OE=8![]() ,则另一直角边AE的长为_____.
,则另一直角边AE的长为_____.
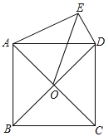
【答案】10;
【解析】
过点O作OM⊥AE于点M,作ON⊥DE,交ED的延长线于点N,易得四边形EMON是正方形,点A,O,D,E共圆,则可得△OEN是等腰直角三角形,求得EN的长,继而证得Rt△AOM≌Rt△DON,得到AM=DN,继而求得答案.
过点O作OM⊥AE于点M,作ON⊥DE,交ED的延长线于点N,
∵∠AED=90°,
∴四边形EMON是矩形,
∵正方形ABCD的对角线交于点O,
∴∠AOD=90°,OA=OD,
∴∠AOD+∠AED=180°,
∴点A,O,D,E共圆,
∴![]() ,
,
∴∠AEO=∠DEO=![]() ∠AED=45°,
∠AED=45°,
∴OM=ON,
∴四边形EMON是正方形,
∴EM=EN=ON,
∴△OEN是等腰直角三角形,
∵OE=8![]() ,
,
∴EN=8,
∴EM=EN=8,
在Rt△AOM和Rt△DON中,
![]() ,
,
∴Rt△AOM≌Rt△DON(HL),
∴AM=DN=EN-ED=8-6=2,
∴AE=AM+EM=2+8=10.
故答案为:10.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,D、E分别是半径OA、OB的中点,C是![]() 上一点,CD=CE.
上一点,CD=CE.
(1)求证:![]() =
=![]() ;
;
(2)若∠AOB=120°,CD=![]() ,求半径OA的长.
,求半径OA的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,矩形
,矩形![]() 的一边落在矩形
的一边落在矩形![]() 的一边上,并且矩形
的一边上,并且矩形![]() ,其相似比为
,其相似比为![]() ,连接
,连接![]() 、
、![]() .
.

![]() 试探究
试探究![]() 、
、![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
![]() 将矩形
将矩形![]() 绕着点
绕着点![]() 按顺时针(或逆时针)旋转任意角度
按顺时针(或逆时针)旋转任意角度![]() ,得到图形
,得到图形![]() 、图形
、图形![]() ,请你通过观察、分析、判断
,请你通过观察、分析、判断![]() 中得到的结论是否能成立,并选取图
中得到的结论是否能成立,并选取图![]() 证明你的判断;
证明你的判断;
![]() 在
在![]() 中,矩形
中,矩形![]() 绕着点
绕着点![]() 旋转过程中,连接
旋转过程中,连接![]() 、
、![]() 、
、![]() ,且
,且![]()
![]() ,
,![]() ,
,![]() 的面积是否存在最大值或最小值?若存在,求出最大值或最小值;若不存在,请说明理由.
的面积是否存在最大值或最小值?若存在,求出最大值或最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
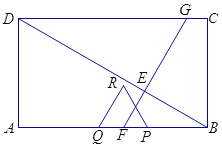
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为对角线
为对角线![]() 上一点,且
上一点,且![]() ,过
,过![]() 作
作![]() ,分别交
,分别交![]() 、
、![]() 于
于![]() 、
、![]() 。动点
。动点![]() 从点
从点![]() 出发,以每秒1个单位长的速度在射线
出发,以每秒1个单位长的速度在射线![]() 上运动。动点
上运动。动点![]() 从点
从点![]() 出发,以每秒1个单位长的速度在线段
出发,以每秒1个单位长的速度在线段![]() 上沿
上沿![]()
![]()
![]() 方向运动。以
方向运动。以![]() 为边作等边
为边作等边![]() 。已知
。已知![]() 、
、![]() 两点同时出发,当点
两点同时出发,当点![]() 返回点
返回点![]() 时两点同时停止运动。运动时间为
时两点同时停止运动。运动时间为![]() 秒.
秒.
(1)求线段![]() ,当点
,当点![]() 落在线段
落在线段![]() 上时
上时![]() 等于多少;
等于多少;
(2)设运动过程中![]() 与矩形
与矩形![]() 的重叠部分面积为
的重叠部分面积为![]() ,请直接写出
,请直接写出![]() 与
与![]() 的函数关系式及自变量
的函数关系式及自变量![]() 的取值范围;
的取值范围;
(3)将四边形![]() 绕点
绕点![]() 旋转一周,在此过程中,设直线
旋转一周,在此过程中,设直线![]() 分别与直线
分别与直线![]() 、
、![]() 交于点
交于点![]() 、
、![]() ,当
,当![]() 是以
是以![]() 为底角的等腰三角形时,求
为底角的等腰三角形时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强校园文化建设,某校准备打造校园文化墙,需用甲、乙两种石材经市场调查,甲种石材的费用![]() (元)与使用面积
(元)与使用面积![]()
![]() 间的函数关系如图所示,乙种石材的价格为每平方米
间的函数关系如图所示,乙种石材的价格为每平方米![]() 元.
元.

(1)求![]() 与
与![]() 间的函数解析式;
间的函数解析式;
(2)若校园文化墙总面积共![]() ,其中使用甲石材
,其中使用甲石材![]()
![]() ,设购买两种石材的总费用为
,设购买两种石材的总费用为![]() 元,请直接写出
元,请直接写出![]() 与
与![]() 间的函数解析式;
间的函数解析式;
(3)在(2)的前提下,若甲种石材使用面积多于![]() ,且不超过乙种石材面积的
,且不超过乙种石材面积的![]() 倍,那么应该怎样分配甲、乙两种石材的面积才能使总费用最少?最少总费用为多少元?
倍,那么应该怎样分配甲、乙两种石材的面积才能使总费用最少?最少总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若干个全等的正五边形排成环状,图中所示的是前3个正五边形,要完成这一圆环还需正五边形的个数为( )

A. 10 B. 9 C. 8 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
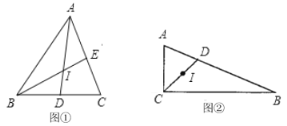
【题目】(1)如图①,小明同学作出![]() 两条角平分线
两条角平分线![]() ,
,![]() 得到交点
得到交点![]() ,就指出若连接
,就指出若连接![]() ,则
,则![]() 平分
平分![]() ,你觉得有道理吗?为什么?
,你觉得有道理吗?为什么?
(2)如图②,![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 的角平分线
的角平分线![]() 上有一点
上有一点![]() ,设点
,设点![]() 到边
到边![]() 的距离为
的距离为![]() .(
.(![]() 为正实数)
为正实数)
小季、小何同学经过探究,有以下发现:
小季发现:![]() 的最大值为
的最大值为![]() .
.
小何发现:当![]() 时,连接
时,连接![]() ,则
,则![]() 平分
平分![]() .
.
请分别判断小季、小何的发现是否正确?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国南水北调中线工程的起点是丹江口水库,按照工程计划,需对原水库大坝进行混凝土培厚加高,使坝高由原来的162米增加到176.6米,以抬高蓄水位,如图是某一段坝体加高工程的截面示意图,其中原坝体的高为BE,背水坡坡角∠BAE=68°,新坝体的高为DE,背水坡坡角∠DCE=60°.求工程完工后背水坡底端水平方向增加的宽度AC.(结果精确到0.1米,参考数据:sin 68°≈0.93,cos 68°≈0.37,tan 68°≈2.5,![]() ≈1.73)
≈1.73)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com