
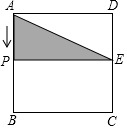
 正方形ABCD的边长为4cm,点E是CD的中点,有一动点P由A出发沿B、C、D方向以2cm/秒的速度匀速运动,直至回到A点停止,设点P运动时间为t秒,当S△AEP=3cm2时,t的值为$\frac{3}{4}$或$\frac{17}{4}$或$\frac{23}{4}$或$\frac{13}{4}$.
正方形ABCD的边长为4cm,点E是CD的中点,有一动点P由A出发沿B、C、D方向以2cm/秒的速度匀速运动,直至回到A点停止,设点P运动时间为t秒,当S△AEP=3cm2时,t的值为$\frac{3}{4}$或$\frac{17}{4}$或$\frac{23}{4}$或$\frac{13}{4}$. 分析 求出DE、EC的长,分为四种情况,分别画出图形,根据面积公式求出即可.
解答 解:∵正方形ABCD的边长为4cm,点E是CD的中点,
∴AD=DC=BC=AB=4cm,DE=CE=2cm,
分为四种情况:
(1)当p在AB上时,如图1,
过E作EF⊥AB于F,
则EF=AD=4cm,
∵S△AEP=3cm2,
∴$\frac{1}{2}×AP×EF$=3cm2,
∴$\frac{1}{2}$×2t×4=3,
解得:t=$\frac{3}{4}$;
(2)当P在BC上时,如图2,
∵S△AEP=3cm2,S△APE=S正方形ABCD-S△ABP-S△ECP-S△ADE,
∴4×4-$\frac{1}{2}$×4×(2t-4)-$\frac{1}{2}$×(8-2t)×2-$\frac{1}{2}×4×2$=3,
解得:t=4.5,
∵2t=9>8,
∴此时P不在BC上,舍去;
(3)当P在DC上时,如图3,
∵S△AEP=3cm2,
∴$\frac{1}{2}$×(2+4+4-2t)×4=3,
解得:t=$\frac{17}{4}$,
当P在DE上时,$\frac{1}{2}$×(2t-2-4-4)×4=3,
此时t=$\frac{23}{4}$;
(4)当P在AD上时,如图4,
∵S△AEP=3cm2,
∴$\frac{1}{2}$×(4+4+4+4-2t)×2=3,
解得:t=$\frac{13}{2}$,
故答案为:$\frac{3}{4}$或$\frac{17}{4}$或$\frac{23}{4}$或$\frac{13}{4}$.
点评 本题考查了正方形的性质,三角形的面积公式的应用,能求出符合的所有情况是解此题的关键.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2+2×2(1+x)=6.62 | B. | 2(1+x)2=6.62 | ||
| C. | 2+2(1+x)+2(1+x)2=6.62 | D. | 2(1+x)(1+2x)=6.62 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com