练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
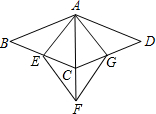
    （2013•丽水）如图，四边形ABCD与四边形AEFG都是菱形，其中点C在AF上，点E，G分别在BC，CD上，若∠BAD=135°，∠EAG=75°，则
    AB
    AE
    =
    		3
    +1
    2
    		3
    +1
    2
    ．
    分析：根据菱形的性质可得出∠BAE=30°，∠B=45°，过点E作EM⊥AB于点M，设EM=x，则可得出AB、AE的长度，继而可得出
    AB
    AE
    的值．
    解答：解：∵∠BAD=135°，∠EAG=75°，四边形ABCD与四边形AEFG都是菱形，
    ∴∠B=180°-∠BAD=45°，∠BAE=∠BAC-∠EAC=30°，
    过点E作EM⊥AB于点M，设EM=x，
    在Rt△AEM中，AE=2EM=2x，AM=
    		3
    x，
    在Rt△BEM中，BM=x，
    则
    AB
    AE
    =
    AM+BM
    AE
    =
    		3
    +1
    2
    ．
    故答案为：
    		3
    +1
    2
    ．
    点评：本题考查了菱形的性质及解直角三角形的知识，属于基础题，关键是掌握菱形的对角线平分一组对角．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （2013•丽水）如图，在Rt△ABC中，∠A=90°，∠ABC的平分线BD交AC于点D，AD=3，BC=10，则△BDC的面积是
    15
    15
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•丽水）如图，AB∥CD，AD和BC相交于点O，∠A=20°，∠COD=100°，则∠C的度数是（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

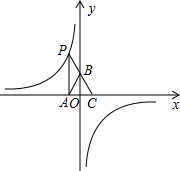    （2013•丽水）如图，点P是反比例函数y=
    k
    x
    （k＜0）图象上的点，PA垂直x轴于点A（-1，0），点C的坐标为（1，0），PC交y轴于点B，连结AB，已知AB=
    		5
    ．
    （1）k的值是
    -4
    -4
    ；
    （2）若M（a，b）是该反比例函数图象上的点，且满足∠MBA＜∠ABC，则a的取值范围是
    0＜a＜2或
    -11-
    		33
    2
    ＜a＜
    -11+
    		33
    2
    0＜a＜2或
    -11-
    		33
    2
    ＜a＜
    -11+
    		33
    2
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

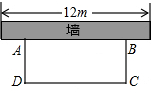    （2013•丽水）如图，科技小组准备用材料围建一个面积为60m2的矩形科技园ABCD，其中一边AB靠墙，墙长为12 m．设AD的长为x m，DC的长为y m．
    （1）求y与x之间的函数关系式；
    （2）若围成矩形科技园ABCD的三边材料总长不超过26m，材料AD和DC的长都是整米数，求出满足条件的所有围建方案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•丽水）如图1，点A是x轴正半轴上的动点，点B坐标为（0，4），M是线段AB的中点，将点M绕点A顺时针方向旋转90°得到点C，过点C作x轴的垂线，垂足为F，过点B作y轴的垂线与直线CF相交于点E，点D是点A关于直线CF的对称点，连结AC，BC，CD，设点A的横坐标为t．
    （1）当t=2时，求CF的长；
    （2）①当t为何值时，点C落在线段BD上；
         ②设△BCE的面积为S，求S与t之间的函数关系式；
    （3）如图2，当点C与点E重合时，将△CDF沿x轴左右平移得到△C′D′F′，再将A，B，C′，D′为顶点的四边形沿C′F′剪开，得到两个图形，用这两个图形拼成不重叠且无缝隙的图形恰好是三角形．请直接写出所有符合上述条件的点C′的坐标．

    查看答案和解析>>

    同步练习册答案