
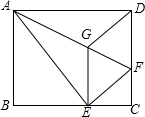
 如图所示,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
如图所示,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.分析 (1)先依据翻折的性质和平行线的性质,证明∠DGF=∠DFG,从而得到GD=DF,接下来依据翻折的性质可证明DG=GE=DF=EF;
(2)连接DE,交AF于点O.由菱形的性质可知GF⊥DE,OG=OF=$\frac{1}{2}$GF,再证明△DOF∽△ADF,由相似三角形的性质可证明DF2=FO•AF,于是可得到GE、AF、FG的数量关系;
(3)依据tan∠FEC=$\frac{3}{4}$,可设CF=3x,CE=4x,进而得到EF=5x,CD=8x=AB,再依据相似三角形对应边成比例,即可得到AE=10x=AD,最后在Rt△ADF中,利用勾股定理列方程求解即可得到矩形ABCD的周长.
解答 解:(1)∵GE∥DF,
∴∠EGF=∠DFG.
∵由翻折的性质可知:GD=GE,DF=EF,∠DGF=∠EGF,
∴∠DGF=∠DFG.
∴GD=DF.
∴DG=GE=DF=EF.
∴四边形EFDG为菱形.
(2)如图,连接DE,交AF于点O.
∵四边形EFDG为菱形,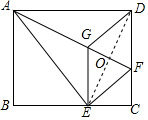
∴GF⊥DE,OG=OF=$\frac{1}{2}$GF.
∵∠DOF=∠ADF=90°,∠OFD=∠DFA,
∴△DOF∽△ADF.
∴$\frac{DF}{AF}$=$\frac{FO}{DF}$,即DF2=FO•AF.
∵FO=$\frac{1}{2}$GF,DF=EG,
∴EG2=$\frac{1}{2}$GF•AF.
(3)∵Rt△CEF中,tan∠FEC=$\frac{3}{4}$,
∴可设CF=3x,CE=4x,则EF=5x=DF,CD=8x=AB,
∵∠B=∠C=90°,∠AEF=∠ADF=90°,
∴∠BAE+∠AEB=∠CEF+∠AEB=90°,
∴∠BAE=∠CEF,
∴△ABE∽△ECF,
∴$\frac{BE}{AB}$=$\frac{CF}{CE}$=$\frac{3}{4}$,即$\frac{BE}{8x}$=$\frac{3}{4}$,
∴BE=6x,
∴BC=10x=AD,
∵Rt△ADF中,AF=5$\sqrt{5}$cm,
∴(10x)2+(5x)2=(5$\sqrt{5}$)2,
解得x=1,
∴AD=10cm,CD=8cm,
∴矩形ABCD的周长=2(10+8)=36cm.
故答案为:36cm.
点评 本题属于相似形综合题,主要考查了相似三角形的判定与性质,矩形的性质以及勾股定理的运用,折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.解决问题的关键是依据直角三角形的勾股定理列方程求解.


 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$≤a≤1 | B. | $\frac{1}{9}$≤a≤2 | C. | $\frac{1}{3}$≤a≤1 | D. | $\frac{1}{3}$≤a≤2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
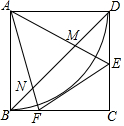 如图,正方形ABCD中,点E,F分别在边CD,BC上,且∠EAF=45°,BD分别交AE,AF于点M,N,以点A为圆心,AB长为半径画弧BD.下列结论:①DE+BF=EF;②BN2+DM2=MN2;③△AMN∽△AFE;④$\widehat{BD}$与EF相切;⑤EF∥MN.其中正确结论的个数是( )
如图,正方形ABCD中,点E,F分别在边CD,BC上,且∠EAF=45°,BD分别交AE,AF于点M,N,以点A为圆心,AB长为半径画弧BD.下列结论:①DE+BF=EF;②BN2+DM2=MN2;③△AMN∽△AFE;④$\widehat{BD}$与EF相切;⑤EF∥MN.其中正确结论的个数是( )| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
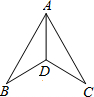 如图,已知∠BAD=∠CAD,图中再补充一个条件后不能说明△ABD≌△ACD,则这个条件是( )
如图,已知∠BAD=∠CAD,图中再补充一个条件后不能说明△ABD≌△ACD,则这个条件是( )| A. | AB=AC | B. | ∠B=∠C | C. | BD=CD | D. | ∠ADB=∠ADC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC内接于半径为5的圆心O,圆心O到弦BC的距离等于3,则tanA等于( )
如图,△ABC内接于半径为5的圆心O,圆心O到弦BC的距离等于3,则tanA等于( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
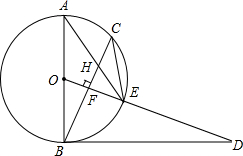 已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com