
【题目】如图,正方形![]() 的边长为
的边长为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() ,
,![]() 上的动点,且
上的动点,且![]() .
.

(1)求证:四边形![]() 是正方形;
是正方形;
(2)求四边形![]() 面积的最小值.
面积的最小值.
【答案】(1)详见解析;(2)四边形![]() 面积的最小值为32.
面积的最小值为32.
【解析】
(1)由正方形的性质得出.∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,证出AH=BE=CF=DG,由SAS证明△AEH≌△BFE≌△CGF≌△DHG,得出EH=FE=GF=GH,
∠AEH=∠BFE,证出四边形EFGH是菱形,再证出∠HEF=90°,即可得出结论;
(2)设四边形EFGH面积为S,AE=xcm,则BE=(8-x)cm,由勾股定理得出S=x2+(8-x)2=2(x-4)2+32,S是x的二次函数,容易得出四边形EFGH面积的最小值.
证明:(1)∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() .
.
∴![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴四边形![]() 是菱形,
是菱形,
∵![]() ,
,![]() ,
,![]() ,
,
∴四边形![]() 是正方形.
是正方形.
(2)设![]() ,
,
则![]() ,
,
S四边形EFGH![]() ,
,
∴当![]() 时,四边形
时,四边形![]() 面积的最小值为32.
面积的最小值为32.


科目:初中数学 来源: 题型:
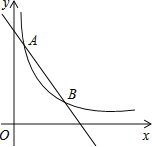
【题目】如图,一次函数y=﹣x+4的图象与反比例函数y=![]() (k为常数,且k≠0)的图象交于A(1,a),B(3,b)两点.
(k为常数,且k≠0)的图象交于A(1,a),B(3,b)两点.
(1)求反比例函数的表达式
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标
(3)求△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明根据学习函数的经验,对函数y=![]() +1的图象与性质进行了探究.下面是小明的探究过程,请补充完整:
+1的图象与性质进行了探究.下面是小明的探究过程,请补充完整:
(1)函数y=![]() +1的自变量x的取值范围是 ;
+1的自变量x的取值范围是 ;
(2)下表列出了y与x的几组对应值,请写出m,n的值:m= ,n= ;
x | … | ﹣ | ﹣1 | ﹣ | 0 |
|
| 2 |
| 3 |
| … |
y | … |
| m |
| 0 | ﹣1 | n | 2 |
|
|
| … |
(3)在如图所示的平面直角坐标系中,描全上表中以各对对应值为坐标的点,并画出该函数的图象.

(4)结合函数的图象,解决问题:
①写出该函数的一条性质:
②当函数值![]() +1>
+1>![]() 时,x的取值范围是:
时,x的取值范围是:
③方程![]() +1=x的解为:
+1=x的解为:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=12cm,BC=16cm,D、E分别是AC、AB的中点,连接DE.点P从点D出发,沿DE方向匀速运动,速度为2cm/s;同时,点Q从点B出发,沿BA方向匀速运动,速度为4cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为t(0<t<4)s.解答下列问题:
(1)当t为何值时,以点E、P、Q为顶点的三角形与△ADE相似?
(2)当t为何值时,△EPQ为等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是矩形
是矩形![]() 内的任意一点,连接
内的任意一点,连接![]() 、
、![]() 、
、![]() 、
、![]() , 得到
, 得到![]() ,
, ![]() ,
, ![]() ,
, ![]() ,设它们的面积分别是
,设它们的面积分别是![]() ,
,![]() ,
,![]() ,
,![]() , 给出如下结论:①
, 给出如下结论:①![]() ②
②![]() ③若
③若![]() ,则
,则![]() ④若
④若![]() ,则
,则![]() 点在矩形的对角线上.其中正确的结论的序号是( )
点在矩形的对角线上.其中正确的结论的序号是( )

A.①②B.②③C.③④D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在直角坐标系中△ABC的顶点A、B、C三点坐标为A(7,1),B(8,2),C(9,0).
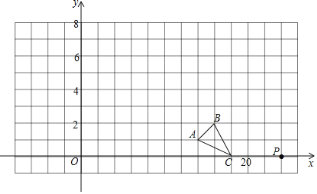
(1)请在图中画出△ABC的一个以点P(12,0)为位似中心,相似比为3的位似图形△A'B'C'(要求与△ABC在P点同一侧);
(2)直接写出A'点的坐标;
(3)直接写出△A'B'C'的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中有4个大小、质地完全相同的乒乓球,球面上分别标有数-1,2,-3,4.
(1)摇匀后任意摸出1个球,则摸出的乒乓球球面上的数是负数的概率为________.
(2)摇匀后先从中任意摸出1个球(不放回),再从余下的3个球中任意摸出1个球,用列表或画树状图的方法求两次摸出的乒乓球球面上的数之和是正数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c的图象与x轴相交于A(﹣1,0),B(3,0)两点,与y轴相交于点C(0,﹣3).
(1)求这个二次函数的表达式;
(2)若P是第四象限内这个二次函数的图象上任意一点,PH⊥x轴于点H,与BC交于点M,连接PC.
①求线段PM的最大值;
②当△PCM是以PM为一腰的等腰三角形时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
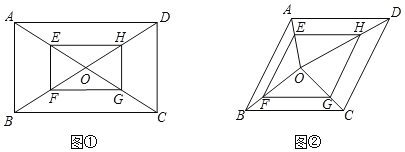
【题目】(教材呈现)
下图是华师版九年级上册数学教材第79页的部分内容.

请根据教材内容,结合图①,写出完整的解题过程.
(结论应用)
(1)在图①中,若AB=2,∠AOD=120°,则四边形EFGH的面积为______.
(2)如图②,在菱形ABCD中,∠BAD=120°,O是其内任意一点,连接O与菱形ABCD各顶点,四边形EFGH的顶点E、F、G、H分别在AO、BO、CO、DO上,EO=2AE,EF∥AB∥GH,且EF=GH,若△EFO与△GHO的面积和为![]() ,则菱形ABCD的周长为______.
,则菱形ABCD的周长为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com