
【题目】二次函数y=ax2+bx+c的图象如图所示,对称轴是x=﹣1,下列结论:(1)ac<0;(2)4ac<b2;(3)2a+b=0;(4)a﹣b+c>2,其中正确的结论共有( ) 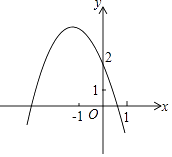
A.1个
B.2个
C.3个
D.4个
【答案】C
【解析】解:由抛物线的开口方向可知:a<0, 由抛物线与y轴交点可知:c>0,
∴ac<0,故①正确;
由抛物线与x轴有两个交点,可知:△>0,
即b2﹣4ac>0,
∴b2>4ac,故②正确;
由于抛物线的对称轴为:x=﹣1
∴﹣ ![]() =﹣1
=﹣1
∴b=2a
∴2a﹣b=0,故③错误;
由于x=0时,y=2,
且x=﹣1时,此时抛物线可取得最大值,
∴当x=﹣1时,y=a﹣b+c>2
故④正确;
故选C.
【考点精析】根据题目的已知条件,利用二次函数图象以及系数a、b、c的关系的相关知识可以得到问题的答案,需要掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE.
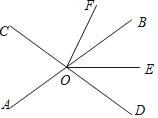
(1)若∠AOC=76°,求∠BOF的度数;
(2)若∠BOF=36°,求∠AOC的度数;
(3)若|∠AOC﹣∠BOF|=α°,请直接写出∠AOC和∠BOF的度数.(用含的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为原点,平行四边形ABCD的边BC在x轴上,D点在y轴上,C点坐标为(2,0),BC=6,∠BCD=60°,点E是AB上一点,AE=3EB,⊙P过D,O,C三点,抛物线y=ax2+bx+c过点D,B,C三点.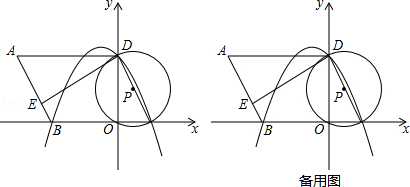
(1)求抛物线的解析式;
(2)说明ED是⊙P的切线,若将△ADE绕点D逆时针旋转90°,E点的对应点E′会落在抛物线上吗?请说明理由;
(3)若点M为此抛物线的顶点,平面上是否存在点N,使得以点B,D,M,N为顶点的四边形为平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1=∠2,那么添加一个条件后,仍无法判定△ABD≌△ACD的是( )
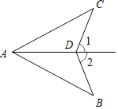
A. AB=AC B. ∠B=∠C C. AD平分∠CAB D. CD=BD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长阳公园有四棵古树A,B,C,D (单位:米).
(1)请写出A,B,C,D四点的坐标;
(2)为了更好地保护古树,公园决定将如图所示的四边形EFGH用围栏圈起来,划为保护区,请你计算保护区的面积.
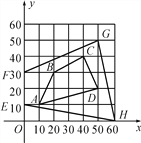
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y= ![]() (k≠0)的图象经过A,B两点,过点A作AC⊥x轴,垂足为C,过点B作BD⊥x轴,垂足为D,连接AO,连接BO交AC于点E,若OC=CD,四边形BDCE的面积为2,则k的值为 .
(k≠0)的图象经过A,B两点,过点A作AC⊥x轴,垂足为C,过点B作BD⊥x轴,垂足为D,连接AO,连接BO交AC于点E,若OC=CD,四边形BDCE的面积为2,则k的值为 . 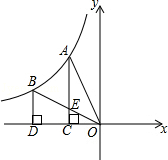
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D为AB的中点,CE=3BE,CF=2AF,四边形CEDF的面积为17,则△ABC的面积为( )
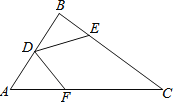
A. 22 B. 23 C. 24 D. 25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,市政府的一项实事工程就是由政府投人1000万元资金对城区4万户家庭的老式水龙头和13L抽水马桶进行免费改造.某社区为配合政府完成该项工作,对社区内1200户家庭中的120户进行了随机抽样调查,并汇总成下表:
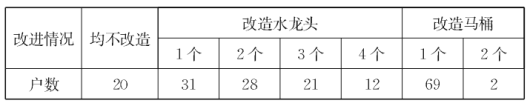
(1)试估计该社区需要对水龙头、马桶进行改造的家庭共有_______户;
(2)改造后,一只水龙头一年大约可节省5t水,一只马桶一年大约可节省15t水,试估计该社区一年共可节约多少吨自来水?
(3)在抽样的120户家庭中,既要改造水龙头又要改造马桶的家庭共有多少户?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com