
 如图,在平面直角坐标系中,若四边形OABC的顶点分别为O(0,0)、A(5,0)、B(m,2)、C(m-5,2).当m的取值范围是1≤m≤9时,在边BC上总存在点P,使∠OPA=90°.
如图,在平面直角坐标系中,若四边形OABC的顶点分别为O(0,0)、A(5,0)、B(m,2)、C(m-5,2).当m的取值范围是1≤m≤9时,在边BC上总存在点P,使∠OPA=90°. 分析 由四边形四个点的坐标易得OA=BC=5,BC∥OA,以OA为直径作⊙D,与直线BC分别交于点E、F,根据圆周角定理得∠OEA=∠OFA=90°,如图1,作DG⊥EF于G,连DE,则DE=OD=2.5,DG=2,根据垂径定理得EG=GF,接着利用勾股定理可计算出EG=1.5,于是得到E(1,2),F(4,2),即点P在E点和F点时,满足条件,此时,当$\left\{\begin{array}{l}{m-5≤4}\\{m≥1}\end{array}\right.$,即1≤m≤9时,边BC上总存在这样的点P,使∠OPA=90°.
解答 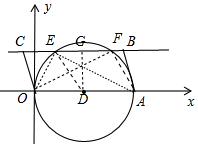 解:∵O(0,0)、A(5,0)、B(m,2)、C(m-5,2).
解:∵O(0,0)、A(5,0)、B(m,2)、C(m-5,2).
∴OA=BC=5,BC∥OA,
以OA为直径作⊙D,与直线BC分别交于点E、F,则∠OEA=∠OFA=90°,
如图,作DG⊥EF于G,连DE,则DE=OD=2.5,DG=2,EG=GF,
∴EG=$\sqrt{D{E}^{2}-D{G}^{2}}$=1.5,
∴E(1,2),F(4,2),
∴当$\left\{\begin{array}{l}{m-5≤4}\\{m≥1}\end{array}\right.$,即1≤m≤9时,边BC上总存在这样的点P,使∠OPA=90°.
故答案为:1≤m≤9.
点评 本题考查了坐标与图形的性质:熟练掌握勾股定理、圆周角定理和平行四边形的判定与性质是解题的关键.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:解答题
 如图,某体育训练基地,有一块边长为(6m+5n)米的正方形土地,现准备在这块正方形土地上修建一个长为(2m+3n)米,宽为(m+2n)米的长方形游泳池,剩余部分则全部修建成休息区域.(结果化简)
如图,某体育训练基地,有一块边长为(6m+5n)米的正方形土地,现准备在这块正方形土地上修建一个长为(2m+3n)米,宽为(m+2n)米的长方形游泳池,剩余部分则全部修建成休息区域.(结果化简)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,动点P从点A出发,沿线段AB运动至点B后,立即按原路返回,点P在运动过程中速度不变,则以点B为圆心,线段BP长为半径的圆的面积S与点P的运动时间t的函数图象大致为( )
如图,动点P从点A出发,沿线段AB运动至点B后,立即按原路返回,点P在运动过程中速度不变,则以点B为圆心,线段BP长为半径的圆的面积S与点P的运动时间t的函数图象大致为( )| A. |  | B. | 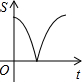 | C. |  | D. | 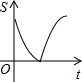 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y随x的增大而增大 | |
| B. | 图象是经过第一、第二象限的一条直线 | |
| C. | 图象向上平移1个单位长度后得到直线y=-2x+1 | |
| D. | 点(1,2)在其图象上 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com