Question

已知△ABC是等腰三角形，过△ABC的一个顶点的一条直线，把△ABC分成两个小三角形，如果这两个小三角形也是等腰三角形，试求出各内角的度数．（不止1个哟!）

Answer 1

一共有4种可能如下：
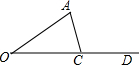
①△ABC是等腰三角形，AB=AC，线段AD是过定点A的，
根据题意，由于△ABD、△ACD是等腰三角形，且AD=BD，AD=CD，
那么∠B=∠BAD=∠CAD=∠C，
利用三角形内角和定理，可知∠B+∠BAD+∠CAD+∠C=180°，
解得∠B=∠BAD=∠CAD=∠C=45°，∠BAC=90°；

②如图所示，①△ABC是等腰三角形，AB=AC，线段AD是过定点A的，
根据题意，由于△ABD、△ACD是等腰三角形，且AB=BD，AD=CD，
那么有∠B=∠C，∠DAC=∠C，∠BAD=∠BDA，所以∠BDA=2∠C，
根据∠B+∠C+∠BAC=180°，可得2∠B+3∠B=180°，
解得∠B=36°，则有∠C=36°，∠BAC=108°；

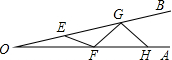
③如图所示，①△ABC是等腰三角形，AB=AC，线段BD是过顶点B的，
根据题意，由于△ABD、△BCD是等腰三角形，且AD=BD，BD=BC，
那么有∠ABC=∠C，∠ABD=∠A，∠BDC=∠C，
利用外角性质有∠BDC=2∠A，再利用三角形内角和定理可得5∠A=180°，
解得∠A=36°，则∠ABC=∠C=72°；

④如图所示，①△ABC是等腰三角形，AB=AC，线段BD是过顶点B的，
根据题意，由于△ABD、△BCD是等腰三角形，且AD=BD，BC=CD，
那么有∠ABC=∠C，∠ABD=∠A，∠DBC=∠CDB，
根据外角性质有∠BDC=2∠A，再结合三角形内角和定理有7∠A=180°，
解得∠A=（

180

7

）°，从而易求∠ABC=∠C=（

540

7

）°．