
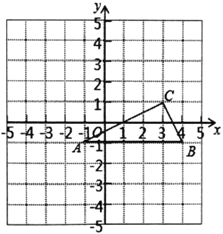
【题目】如图,![]() 的三个顶点在边长为1的正方形网格中,已知
的三个顶点在边长为1的正方形网格中,已知![]() ,
,![]() ,
,![]() .
.
(1)画出![]() 关于
关于![]() 轴对称的
轴对称的![]() (其中
(其中![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() 的对应点,不写画法);
的对应点,不写画法);
(2)分别写出![]() ,
,![]() ,
,![]() 三点的坐标.
三点的坐标.
(3)请写出所有以![]() 为边且与
为边且与![]() 全等的三角形的第三个顶点(不与
全等的三角形的第三个顶点(不与![]() 重合)的坐标_____.
重合)的坐标_____.
【答案】(1)见解析;(2)A′(1,-1),B′(-4,-1),C′(-3,1);(3)(0,1)或(0,-3)或(3,-3)
【解析】
(1)根据网格结构找出点A、B、C关于y轴的对称点A′、B′、C′的位置,然后顺次连接即可;
(2)根据平面直角坐标系写出各点的坐标即可;
(3)利用轴对称性确定出另一个点,然后根据平面直角坐标系写出坐标即可.
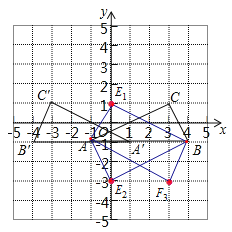
解:(1)△A′B′C′如图所示;
(2)A′(1,-1),B′(-4,-1),C′(-3,1);
(3)如图,第三个点的坐标为(0,1)或(0,-3)或(3,-3).
在△ABC和△BAE1中,
∵BC=AE1=![]() ,
,
AC=BE1=![]() ,
,
AB=BA,
∴△ABC≌△BAE1,
同理可证:△ABC≌△BAE2,△ABC≌△ABE3.


 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案科目:初中数学 来源: 题型:
【题目】阅读理解与应用:对式子x2+2x-3变形如下:x2+2x-3=x2+2x+1-1-3=(x2+2x+1)-4=(x+1)2-4.像这种变形抓住了完全平方公式的特点,先在原式中添加一项,使其中的三项成为完全平方式,再减去添加的这项,我们把这种恒等变形叫配方. 配方法是一种用来把二次多项式化为一个一次多项式的平方与一个常数的和的方法,它的应用十分广泛.请你尝试解决下列问题:
(1)对式子x2-2x+2020进行配方;
(2)已知2y-2x2-8x=y+10,求y的最小值;
(3)如图,在足够大的空地上有一段长为a(a≥250)米的旧墙MN,某人利用旧墙和木栏围成一个长方形菜园ABCD,其中 AD≤MN,已知长方形菜园的一边靠墙,另三边一共用了100米木栏. 求长方形菜园ABCD面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(0,b),点B(a,0),点D(-2,0),其中a、b满足![]() , DE⊥x轴,且∠BED=∠ABO,直线AE交x轴于点C.
, DE⊥x轴,且∠BED=∠ABO,直线AE交x轴于点C.
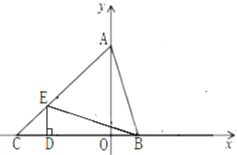
⑴ 分别求出点A、B的坐标;
⑵ 求证:△AOB≌△BDE,并求出点E的坐标
⑶ 若以AB为腰在第一象限内构造等腰直角△ABF,直接写出点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知矩形AOBC的顶点C的坐标是(2,4),动点P从点A出发,沿线段AO向终点O运动,同时动点Q从点B出发,沿线段BC向终点C运动.点P、Q的运动速度均为1个单位,运动时间为t秒.过点P作PE⊥AO交AB于点E.
(1)求直线AB的解析式;
(2)设△PEQ的面积为S,求S与t时间的函数关系,并指出自变量t的取值范围;
(3)在动点P、Q运动的过程中,点H是矩形AOBC内(包括边界)一点,且以B、Q、E、H为顶点的四边形是菱形,直接写出t值和与其对应的点H的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,现有下列结论:①b2﹣4ac>0 ②a>0 ③b>0 ④c>0 ⑤9a+3b+c<0,则其中结论正确的个数是( )
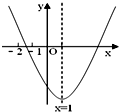
A、2个B、3个
C、4个D、5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,已知AB=AC,D是AC上的一点,CD=9,BC=15,BD=12.

(1)证明:△BCD是直角三角形.
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读探索
问题背景:著名数学家华罗庚提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其他星球“人”进行第一次”谈话“的语言.2002年8月在北京召开的国际数学大会会标取材于我国古代数学家赵爽的《勾股圆方图注》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图1所示).勾股定理是一条古老的数学定理,它有很多种证明方法,我国汉代数学家赵爽根据弦图,利用面积进行了证明.
赵爽证明方法如下:
以a、b为直角边(b>a),以c为斜边作四个全等的直角三角形,则每个直角三角形的面积等于![]() ,把这四个直角三角形拼成如图1所示形状.
,把这四个直角三角形拼成如图1所示形状.
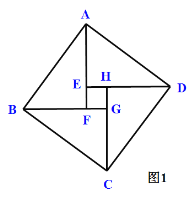
∵Rt△DAE≌Rt△ABF
∴∠EDA=∠FAB
∵∠EAD+∠EDA=90°
∴∠FAB+∠EAD=90°
∴四边形ABCD是一个边长为c的正方形,它的面积等于![]()
∵EF=FG=GH=HE=b-a
∠HEF=90°
∴四边形EFGH是一个边长为b-a的正方形,它的面积等于![]()
∴![]()
∴![]() 从而证明了勾股定理.
从而证明了勾股定理.
思维拓展:
1、如果大正方形的面积为13,小正方形的面积为1,直角三角形的较短直角边长为a,较长直角边长为b,那么![]() 的值为 .
的值为 .
2、美国第二十届总统加菲尔德也曾经给出了勾股定理的一种证明方法,如图2所示,
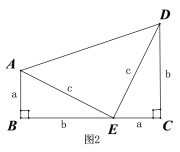
他用两个全等的直角三角形和一个等腰直角三角形拼出了一个直角梯形,请你利用此图形验证勾股定理.
证明:∵直角梯形ABCD的面积可以用两种方法表示:
第一种方法表示为:
第二种方法表示为:
∴ =
∴![]()
探索创新:
用纸做成四个全等的直角三角形,两直角边的长分别为a和b,斜边长为c,请你开动脑筋,将它们拼成一个能证明勾股定理的图形(不同于上面图1和图2).请画出你拼成的图形,并用你画的图形证明勾股定理.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.
(1)求y与x的函数关系式;
(2)若在购买计划中,B种苗的数量不超过35棵,但不少于A种苗的数量,请设计购买方案,使总费用最低,并求出最低费用.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】天猫网的新时代书店准备购进甲、乙两种图书,已知甲种图书进价比乙种图书贵4元,用3000元购进甲种图书的数量与用2400元购进乙种图书的数量相同.
(1)甲、乙两种图书的单价分别为多少元?
(2)若甲种图书每本售价30元,乙种图书每本售价25元,书店欲同时购进两种图书共100本,请写出所获利润y(单位:元)关于甲种图书x(单位:本)的函数解析式;
(3)在(2)的条件下,若书店计划用不超过1800元购进两种图书,且甲种图书至少购进40本,并将所购图书全部销售,共有多少种购进方案?哪一种方案利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com