
 如图,一圆柱体的底面圆周长为20cm,高AB为4cm,BC是上底的直径,一只蚂蚁从点A出发,沿着圆柱的表面爬行到点C,则爬行的最短路程是( )
如图,一圆柱体的底面圆周长为20cm,高AB为4cm,BC是上底的直径,一只蚂蚁从点A出发,沿着圆柱的表面爬行到点C,则爬行的最短路程是( )| A. | 2$\sqrt{29}$ | B. | $\frac{4}{π}$$\sqrt{{π}^{2}+25}$ | C. | 2$\sqrt{25{π}^{2}+4}$ | D. | 14 |
科目:初中数学 来源: 题型:解答题
| 空气污染指数(ω) | 30 | 40 | 70 | 80 | 90 | 110 | 120 | 140 |
| 天数(t) | 1 | 2 | 3 | 5 | 7 | 6 | 4 | 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
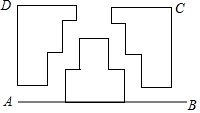 如图,四边形ABCD是一块长方形场地,AB=42米,AD=25米,从A,B两处入口的小路宽都为1米,两小路回合处路宽为2米,其余部分种植草坪,则草坪面积为960平方米.
如图,四边形ABCD是一块长方形场地,AB=42米,AD=25米,从A,B两处入口的小路宽都为1米,两小路回合处路宽为2米,其余部分种植草坪,则草坪面积为960平方米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (0,10) | B. | (5,0) | C. | (0,-5) | D. | (0,4) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com