
【题目】已知抛物线![]() .
.
(1)用配方法求它的顶点坐标、对称轴;
(2)当![]() 的值在什么范围内时,
的值在什么范围内时,![]() 随
随![]() 的增大而增大?当
的增大而增大?当![]() 的值在什么范围内时,
的值在什么范围内时,![]() 随
随![]() 的增大而减小?
的增大而减小?
(3)当![]() 的值在什么范围内时,抛物线在
的值在什么范围内时,抛物线在![]() 轴上方?
轴上方?
 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】已知O为坐标原点,抛物线y=x2﹣3x﹣4与x轴交于A,B两点(点A在点B的右侧),有点C(﹣2,6).
(1)求A,B两点的坐标.
(2)若点D(1,﹣3),点E在线段OA上,且∠ACB=∠ADE,延长ED交y轴于点F,求△EFO的面积.
(3)若M在直线AC上,点Q在抛物线上,是否存在点M和点N,使以Q,M,N,A为顶点的四边形是正方形?若存在,直接写出M点的坐标.若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
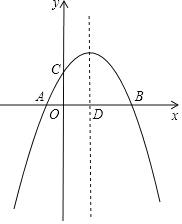
【题目】如图,抛物线y=ax2+![]() x+c(a≠0)与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知点A的坐标为(﹣1,0),点C的坐标为(0,2).
x+c(a≠0)与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知点A的坐标为(﹣1,0),点C的坐标为(0,2).
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
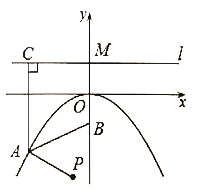
【题目】如图,抛物线![]() 经过点
经过点![]() .点
.点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作直线
作直线![]() 轴,点
轴,点![]() 是抛物线
是抛物线![]() 上一点,
上一点,![]() 于点
于点![]() .
.
![]() 求抛物线解析式:
求抛物线解析式:
![]() 在抛物线对称轴上是否存在一定点
在抛物线对称轴上是否存在一定点![]() ,使得
,使得![]() 永远成立?若存在,求出点
永远成立?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
![]() 若点
若点![]() 坐标为
坐标为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西省第十五届运动会乒乓球比赛于2018年8月13日上午在山西省体育博物馆的比赛场馆内正式拉开了帷幕.第十五届运动会竞技体育组乒乓球项目产生的决赛运动员名单中太原市共27人,其中甲组有甲、乙、丙、丁四名女子运动员,若进行一次乒乓球单打比赛,要通过抽签从中选出两名运动员打第一场比赛.
(1)若已确定甲打第一场,再从其余三名运动员中随机选取一位,求恰好选中乙的概率;
(2)若两名运动员都不确定,请用树状图法或列表法,求恰好选中甲、乙两名运动员的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
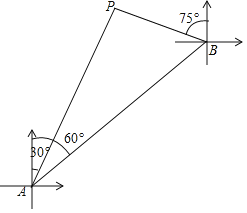
【题目】如图,一艘轮船在A处测得灯塔P在船的北偏东30°方向,轮船沿着北偏东60°方向航行16km后到达B处,这时灯塔P在船的北偏西75°方向.则灯塔P与B之间的距离等于___________km(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】武汉某中学开展了周末网课学习活动,为了解学生网课学习效果进行了抽样测试,该校教导处把测试结果分为A(优秀)、B(良好)、C(不合格)三种类型.如图是对该校初一(1)班和初一(2)班全体同学进行测试后绘制的两幅不完整的统计图,请根据图中信息解答下列问题.
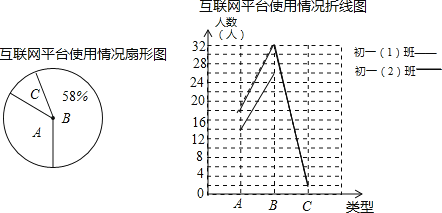
(1)此次被调查的学生总人数是 人;扇形统计图中代表类型C的扇形的圆心角为 ;
(2)补全折线统计图;
(3)如果该校初一年级学生共有1200人,试根据此次调查结果估计该校初一年级中C类学生约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,过O点作OP⊥AB,交弦AC于点D,交⊙O于点E,且使PC是⊙O的切线.
(1)求证:∠PCA=∠ABC;
(2)若∠P=60°,PC=4,求PE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com