
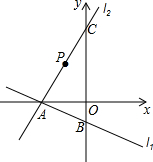
 ��ֱ֪��l1�Ľ���ʽΪy=-$\frac{1}{3}$x-2������x�ᣬy��ֱ���A��B���㣬��C��y���ϣ��ҵ�C��������Ϊx2-7x-8=0�нϴ�Ľ⣬ֱ��l2��A��C���㣮
��ֱ֪��l1�Ľ���ʽΪy=-$\frac{1}{3}$x-2������x�ᣬy��ֱ���A��B���㣬��C��y���ϣ��ҵ�C��������Ϊx2-7x-8=0�нϴ�Ľ⣬ֱ��l2��A��C���㣮���� ��1�������Ա����뺯��ֵ�Ķ�Ӧ��ϵ���ɵ�A��B�����꣬���ݽⷽ�̣��ɵ�C�����꣬���ݴ���ϵ�������ɵú�������ʽ��
��2����������ĺͲ�ɵ�P�����꣬���ݴ���ϵ�������ɵ÷�������������ʽ��
��3���������ۣ���AP=PBʱ����AB=APʱ����AB=BPʱ�����ݹ��ɶ������ɵù���a�ķ��̣����ݽⷽ�̣��ɵ�P�����꣬�ٸ��ݹ��ɶ������ɵô𰸣�
��� �⣺��1����x=0ʱ��y=-2����B�������ǣ�0��-2����
��y=0ʱ��-$\frac{1}{3}$x-2-0�����x=-6����A�������ǣ�-6��0����
x2-7x-8=0��
��ʽ�ֽ⣬�ã�x-8����x+1��=0��
���x=8��x=-1��
C��������0��8����
��ֱ��l2�Ľ���ʽΪy=kx+b��ֱ��l2��A��C���㣬��
$\left\{\begin{array}{l}{b=8}\\{-6k+b=0}\end{array}\right.$��
���$\left\{\begin{array}{l}{b=8}\\{k=\frac{4}{3}}\end{array}\right.$��
��ֱ��l2�Ľ���ʽΪy=$\frac{4}{3}$x+8��
��2����P��a��b����������ĺͲ��
S��ABP=S��ABC-S��BCP��
��$\frac{1}{2}$��[8-��-2��]��|-6|-$\frac{1}{2}$[8-��-2��]|x|=20��
���x=-2��x=2������������Ҫ��ȥ����
b=$\frac{4}{3}$����-2��+8=$\frac{16}{3}$��
��P��-2��$\frac{16}{3}$����
�����P�ķ�������������ʽΪy=$\frac{{k}_{1}}{x}$����P��������룬��
k1=-2��$\frac{16}{3}$=-$\frac{32}{3}$��
�ʹ���P�ķ�������������ʽΪy=-$\frac{\frac{32}{3}}{x}$��
��3���ٵ�AP=PBʱ��P��C���غϣ���t=0��
�ڵ�AB=APʱ��AP=AB=$\sqrt{��-6��^{2}+��0+2��^{2}}$=2$\sqrt{10}$��PC=AC-AP=10-2$\sqrt{10}$��
�۵�AB=BPʱ����P��a��$\frac{4}{3}$a+8����a2+��$\frac{4}{3}$a+8+2��2=��-6��2+22��
����
5a2+48a+108=0�����a=-6.2������������Ҫ��ȥ��a=-3.4��
$\frac{4}{3}$a+8=$\frac{52}{15}$����P��-$\frac{17}{5}$��$\frac{52}{15}$����
PC=$\sqrt{��-\frac{17}{5}��^{2}+��8-\frac{52}{15}��^{2}}$=$\frac{17}{3}$��
��t=$\frac{17}{3}$��
����������t=0��t=10-2$\sqrt{10}$��t=$\frac{17}{3}$��A��B��P���������������������
���� ���⿼����һ�κ����ۺ��⣬��1�������˺���ֵ���Ա����Ķ�Ӧ��ϵ������ϵ������������ʽ����2����������ĺͲ�ó�P�������ǽ���ؼ�����3�����������ǽ���ؼ����Է���©��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
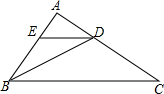 ��ͼ���ڡ�ABC�У�BDƽ�֡�ABC��DEƽ�֡�ADB����DE��BC��
��ͼ���ڡ�ABC�У�BDƽ�֡�ABC��DEƽ�֡�ADB����DE��BC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
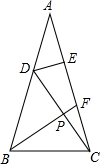 ��ͼ��ABC�У���A=36�㣬AB=AC��BFƽ�֡�ABC��E��AF���е㣬DE��AC��AB��D������DC��BF��P����DPB�Ķ����ǣ�������
��ͼ��ABC�У���A=36�㣬AB=AC��BFƽ�֡�ABC��E��AF���е㣬DE��AC��AB��D������DC��BF��P����DPB�Ķ����ǣ�������| A�� | 36�� | B�� | 54�� | C�� | 72�� | D�� | 90�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
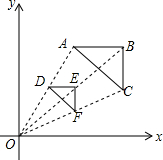 ��ͼ����ABC�У�A��2��4����ԭ��Ϊλ�����ģ�����ABC��С��õ���DEF����D��1��2������DEF�����Ϊ4�����ABC�����Ϊ��������
��ͼ����ABC�У�A��2��4����ԭ��Ϊλ�����ģ�����ABC��С��õ���DEF����D��1��2������DEF�����Ϊ4�����ABC�����Ϊ��������| A�� | 2 | B�� | 4 | C�� | 8 | D�� | 16 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �����Խ����ഹֱ��� | B�� | һ��Ա���ȣ�һ��Խ���� | ||
| C�� | һ��Ա�ƽ�У���һ��Ա���� | D�� | һ��Ա�ƽ�У�һ��Խ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{x}^{2}}{2}$ | B�� | $\frac{x}{x+1}$ | C�� | $\frac{x}{2}$+y | D�� | $\frac{x}{3}$+1 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com