
如果三角形有一边上的中线恰好等于这边的长,那么称这个三角形为“匀称三角形”.
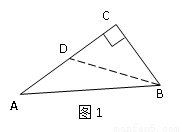
(1)已知:如图1,在△ABC中,∠C=90°,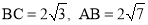 .
.
求证:△ABC是“匀称三角形”;
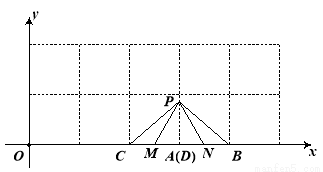
(2)在平面直角坐标系xoy中,如果三角形的一边在x轴上,且这边的中线恰好等于这边的长,我们又称这个三角形为“水平匀称三角形”.如图2,现有10个边长是1的小正方形组成的长方形区域记为G, 每个小正方形的顶点称为格点,A(3,0),B(4,0),若C、D(C、D两点与O不重合)是x轴上的格点,且点C在点A的左侧.在G内使△PAC与△PBD都是“水平匀称三角形”的点P共有几个?其中是否存在横坐标为整数的点P,如果存在请求出这个点P的坐标,如果不存在请说明理由.
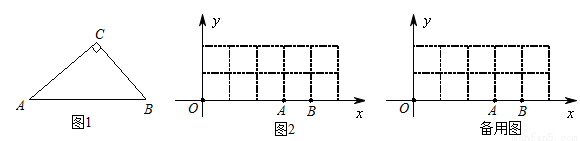
(1)证明见解析;(2)4个,存在,(3,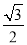 ).
).
【解析】
试题分析:(1)应用勾股定理求出AC和它的中线长,根据匀称三角形的定义即可证得.
(2)根据匀称三角形的定义求解即可.
试题解析:(1) 如图1,作AC边的中线BD交AC于点D,
∵∠C=90°,BC= 2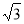 ,AB = 2
,AB = 2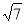 ,∴AC =
,∴AC = 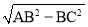 = 4.
= 4.
∴AD=CD=2,BD =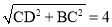 .∴AC = BD.
.∴AC = BD.
∴ △ABC是“匀称三角形”.
(2)①在G内使△PAC与△PBD都是“水平匀称三角形”的点P共有4个 .
②在G内使△PAC与△PBD都是“水平匀称三角形”的点P中,存在横坐标为整数的点P.
如图,当C点坐标为(2,0),D点坐标为(3,0)与A重合时,△PAC与△PBD是水平匀称三角形.
∵A(3,0),C(2,0),B(4,0),D(3,0),∴AC=1,BD=1.
设PM、PN分别为CA、DB上的中线,
∴AM=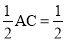 ,AN=
,AN=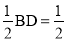 , ∴AM=AN=
, ∴AM=AN=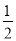 .
.
∴点A为MN的中点.
∵△PAC与△PBD是“水平匀称三角形”,
∴PM=AC=1,PN=BD=1.∴PM=PN=1.
∴PA⊥MN,即PA与x轴垂直.
∵A(3,0),∴P点横坐标为整数3.
在Rt△PMA中,PM=1,AM=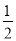 ,∴PA=
,∴PA=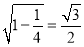 .
.
∴P(3,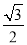 ).
).
∴当C点坐标为(2,0),D点坐标为(3,0)与A重合时,△PAC与△PBD是水平匀称三角形且P点横坐标为整数.
考点:1.新定义和阅读理解型问题;2.勾股定理;3.点的坐标.


 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源:2013-2014学年北京市昌平区中考一模数学试卷(解析版) 题型:填空题
已知:四边形ABCD的面积为1. 如图1,取四边形ABCD各边中点,则图中阴影部分的面积为 ;如图2,取四边形ABCD各边三等分点,则图中阴影部分的面积为 ;如图3,取四边形ABCD各边的n(n为大于1的整数)等分点,则图中阴影部分的面积为 .

查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市大兴区中考一模数学试卷(解析版) 题型:解答题
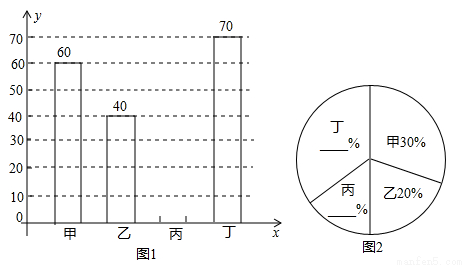
某中学开展“绿化家乡、植树造林”活动,为了解全校植树情况,对该校甲、乙、丙、丁四个班级植树的棵树和所占百分比情况进行了调查,将收集的数据整理并绘制成图1和图2两幅不完整的统计图,请根据图中的信息,完成下列问题:
(1)这四个班共植树 棵;
(2)请补全两幅统计图;
(3)若四个班级植树的平均成活率是95%,全校共植树2000棵,请你估计全校种植的树中成活的树大约有多少棵?
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市大兴区中考一模数学试卷(解析版) 题型:解答题
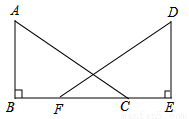
已知:如图,点B、F、C、E在同一直线上,BF=CE,AB⊥BE,DE⊥BE,垂足分别为B、E,联结AC、DF,∠A=∠D.
求证:AB=DE.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市丰台区中考二模数学卷(解析版) 题型:解答题
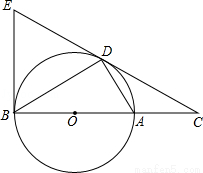
如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD2=CA•CB;
(2)求证:CD是⊙O的切线;
(3)过点B作⊙O的切线交CD的延长线于点E,若BC=12,tan∠CDA=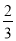 ,求BE的长.
,求BE的长.
查看答案和解析>>
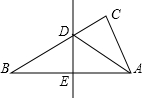
科目:初中数学 来源:2013-2014学年内蒙古满洲里市九年级三月月考数学试卷(解析版) 题型:选择题
右边的图形是由8个棱长为1个单位的小立方体组成的立体图形,这个立体图形的主视图是( )

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.2 | B.3 | C.4 | D.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com