
【题目】如图,过反比例函数y= ![]() (x>0)的图象上任意两点A、B分别作x轴的垂线,垂足分别为C、D,连接OA、OB,设AC与OB的交点为E,△AOE与梯形ECDB的面积分别为S1、S2 , 比较它们的大小,可得( )
(x>0)的图象上任意两点A、B分别作x轴的垂线,垂足分别为C、D,连接OA、OB,设AC与OB的交点为E,△AOE与梯形ECDB的面积分别为S1、S2 , 比较它们的大小,可得( ) 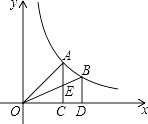
A.S1>S2
B.S1=S2
C.Sl<S2
D.大小关系不能确定
科目:初中数学 来源: 题型:
【题目】如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距100(![]() +1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
+1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
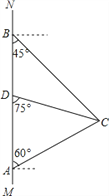
(1)分别求出A与C,A与D间的距离AC和AD(如果运算结果有根号,请保留根号).
(2)已知距离观测点D处100海里范围内有暗礁,若巡逻船A沿直线AC去营救船C,在去营救的途中有无触礁的危险?(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应政府提出的“绿色发展·低碳出行”号召,某社区决定购置一批共享单车,经市场调查得知,购买3量男式单车与4辆女式单车费用相同,购买5辆男式单车与4辆女式单车共需16000元.
(1)求男式单车和女式单车的单价;
(2)该社区要求男式单比女式单车多4辆,两种单车至少需要22辆,购置两种单车的费用不超过50000元,该社区有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将平行四边形纸片ABCD按如图方式折叠,使点C与A重合,点D落到D′处,折痕为EF.

(1)求证:△ABE≌△AD′F;
(2)连接CF,判断四边形AECF是什么特殊四边形?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列诗句表述的是随机事件的是( )
A.离离原上草,一岁一枯荣B.危楼高百尺,手可摘星辰
C.会当凌绝顶,一览众山小D.东边日出西边雨,道是无晴却有晴
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=ax+b(a≠0)、二次函数y=ax2+bx和反比例函数y=![]() (k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(-2,0),则下列结论中,正确的是( )
(k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(-2,0),则下列结论中,正确的是( )

A.b=2a+k B.a=b+k C.a>b>0 D.a>k>0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC与BD交于点O,AC=6,BD=8.动点E从点B出发,沿着B﹣A﹣D在菱形ABCD的边上运动,运动到点D停止.点F是点E关于BD的对称点,EF交BD于点P,若BP=x,△OEF的面积为y,则y与x之间的函数图象大致为( )

A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com