
【题目】已知:如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,CM是斜边AB上的中线,将△ACM沿直线CM折叠,点A落在点A1处,CA1与AB交于点N,且AN=AC,则∠A的度数是( )
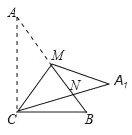
A. 30° B. 36° C. 50° D. 60°
科目:初中数学 来源: 题型:
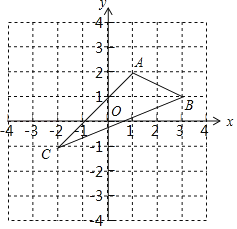
【题目】如图,在平面直角坐标系中,已知A(1,2),B(3,1),C(﹣2,﹣1).
(1)在图中作出△ABC关于y轴对称的△A1B1C1.
(2)直接写出点A1,B1,C1的坐标.
A1 , B1 , C1 ;
(3)请你求出△A1B1C1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】首都国际机场连续五年排名全球最繁忙机场第二位,该机场2012﹣2016年客流量统计结果如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
客流量(万人次) | 8192 | 8371 | 8613 | 8994 | 9400 |
根据统计表中提供的信息,预估首都国际机场2017年客流量约万人次,你的预估理由是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠D=90°,AC平分∠DAB,且点C在以AB为直径的⊙O上. 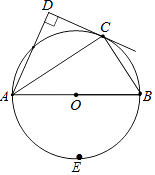
(1)求证:CD是⊙O的切线;
(2)点E是⊙O上一点,连接BE,CE.若∠BCE=42°,cos∠DAC= ![]() ,AC=m,写出求线段CE长的思路.
,AC=m,写出求线段CE长的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,点E是对角线AC上的动点(与点A,C不重合),连接BE.
(1)将射线BE绕点B顺时针旋转45°,交直线AC于点F.
①依题意补全图1;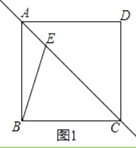
②小研通过观察、实验,发现线段AE,FC,EF存在以下数量关系:
AE与FC的平方和等于EF的平方.小研把这个猜想与同学们进行交流,通过讨论,形成证明该猜想的几种想法:
想法1:将线段BF绕点B逆时针旋转90°,得到线段BM,要证AE,FC,EF的关系,只需证AE,AM,EM的关系.
想法2:将△ABE沿BE翻折,得到△NBE,要证AE,FC,EF的关系,只需证EN,FN,EF的关系.
…
请你参考上面的想法,用等式表示线段AE,FC,EF的数量关系并证明;(一种方法即可)
(2)如图2,若将直线BE绕点B顺时针旋转135°,交直线AC于点F.小研完成作图后,发现直线AC上存在三条线段(不添加辅助线)满足:其中两条线段的平方和等于第三条线段的平方,请直接用等式表示这三条线段的数量关系.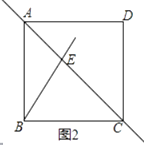
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEF中,已有条件AB=DE,还需要添加两个条件才能使△ABC≌△DEF.不能添加的一组条件是( )
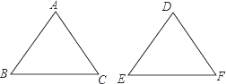
A. ∠B=∠E,BC=EF B. ∠A=∠D,BC=EF
C. ∠A=∠D,∠B=∠E D. BC=EF,AC=DF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△A1B1C1,△A2B2C2的周长相等,现有两个判断:
①若A1B1=A2B2,A1C1=A2C2,则△A1B1C1≌△A2B2C2;
②若∠A1=∠A2,∠B1=∠B2,则△A1B1C1≌△A2B2C2,
对于上述的两个判断,下列说法正确的是( )
A. ①正确,②错误 B. ①错误,②正确 C. ①,②都错误 D. ①,②都正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE,设∠BAD=α,∠CDE=β.
(1)如图,若点D在线段BC上,点E在线段AC上.
①如果∠ABC=60°,∠ADE=70°,那么α=°,β=°.②求α,β之间的关系式.
(2)是否存在不同于以上②中的α,β之间的关系式?若存在,请求出这个关系式(求出一个即可);若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“经过已知直线外一点作这条直线的平行线”的尺规作图过程.
已知:如图1,直线l和直线l外一点P.
求作:直线l的平行直线,使它经过点P.
作法:如图2.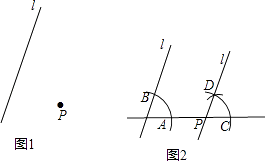
(i)过点P作直线m与直线l交于点O;
(ii)在直线m上取一点A(OA<OP),以点O为圆心,OA长为半径画弧,与直线l交于点B;
(iii)以点P为圆心,OA长为半径画弧,交直线m于点C,以点C为圆心,AB长为半径画弧,两弧交于点D;
(iv)作直线PD.
所以直线PD就是所求作的平行线.
请回答:该作图的依据是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com