
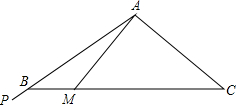
 在等腰△ABC中AB=AC,∠BAC=120°,在边AB的延长线上有一点P,射线AP从AB开始,绕点A逆时针匀速旋转,每秒钟旋转15°,到达AC后立即以相同旋转速度返回AB,到达后立即重复上述旋转过程.当AP旋转1秒时,此时光线AP交BC于点M,BM的长为(20$\sqrt{3}$-20)cm,光线AP从AB处旋转开始计时,若要转2018秒,射线AP与BC边的交点与点B之间的距离是(20$\sqrt{3}$-10)cm.
在等腰△ABC中AB=AC,∠BAC=120°,在边AB的延长线上有一点P,射线AP从AB开始,绕点A逆时针匀速旋转,每秒钟旋转15°,到达AC后立即以相同旋转速度返回AB,到达后立即重复上述旋转过程.当AP旋转1秒时,此时光线AP交BC于点M,BM的长为(20$\sqrt{3}$-20)cm,光线AP从AB处旋转开始计时,若要转2018秒,射线AP与BC边的交点与点B之间的距离是(20$\sqrt{3}$-10)cm. 分析 过A点作AD⊥BC,垂足为D,设AB=2tcm,在Rt△ABD中,AD=$\frac{1}{2}$AB=t,BD=$\frac{\sqrt{3}}{2}$AB=$\sqrt{3}$t,在Rt△AMD中,∠AMD=∠ABC+∠BAM=45°,即MD=AD=t,由BM=BD-MD列出方程解得t=20,从而求出AB、BD、AD的长,再设光线AP旋转2018秒后光线与BC的交点为Q,由题意可知,光线从边AB开始到第一次回到AB处需8×2=16秒,而2018=126×16+2,即AP旋转2018秒与旋转2秒时和BC的交点是同一个点Q,得出∠BAQ=30°,求出DQ、CQ的长,即可得出结果.
解答 解:过A点作AD⊥BC,垂足为D,如图所示:
∵∠BAC=120°,AB=AC,
∴∠ABC=∠C=30°,
设AB=2tcm,
在Rt△ABD中,AD=$\frac{1}{2}$AB=t,BD=$\frac{\sqrt{3}}{2}$AB=$\sqrt{3}$t,
在Rt△AMD中,∵∠AMD=∠ABC+∠BAM=45°,
∴MD=AD=t,
∵BM=BD-MD.即$\sqrt{3}$t-t=20$\sqrt{3}$-20.
解得t=20,
∴AB=2×20=40cm,BD=$\frac{1}{2}$BC=20$\sqrt{3}$cm,AD=20cm,
设光线AP旋转2018秒后光线与BC的交点为Q,
由题意可知,120÷15=8,光线从边AB开始到第一次回到AB处需8×2=16秒,
而2018=126×16+2,即AP旋转2018秒与旋转2秒时和BC的交点是同一个点Q,
∴∠BAQ=30°,则∠QAD=30°,
∴在Rt△ADQ中,DQ=$\frac{1}{2}$AD=10cm,
∴CQ=CD+DQ=BD+DQ=20$\sqrt{3}$+10(cm),
BQ=BC-CQ=2BD-CQ=2×20$\sqrt{3}$-20$\sqrt{3}$-10=20$\sqrt{3}$-10(cm),
∴光线AP旋转2018秒后,与BC的交点与点B之间的距离为20$\sqrt{3}$-10(cm);
故答案为:(20$\sqrt{3}$-10)cm.
点评 本题考查了旋转的性质、等腰三角形的性质、含30°角直角三角形的性质、三角函数等知识;熟练掌握旋转的性质与直角三角形的性质时解决问题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 观察下列各个等式:
观察下列各个等式:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在Rt△ABC中,∠C=90°,∠A=30°,点P在AC边上,以点P为中心,将△ABC顺时针旋转90°,得到△DEF,DE交边AC于G,当P为中点时,AG:DG的值为$\frac{\sqrt{3}-1}{2}$.
如图,在Rt△ABC中,∠C=90°,∠A=30°,点P在AC边上,以点P为中心,将△ABC顺时针旋转90°,得到△DEF,DE交边AC于G,当P为中点时,AG:DG的值为$\frac{\sqrt{3}-1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,两个完全一样的正方形ABOC和正方形DEMF,正方形DEMF的顶点E与正方形ABOC的中心重合,将正方形DEMF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,射线EF与线段AB相交于点G,与射线CA相交于点Q.若AQ=12,BP=3,则PG=5.
如图所示,两个完全一样的正方形ABOC和正方形DEMF,正方形DEMF的顶点E与正方形ABOC的中心重合,将正方形DEMF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,射线EF与线段AB相交于点G,与射线CA相交于点Q.若AQ=12,BP=3,则PG=5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com