Question

某服装店以每件40元的价格购进一批衬衫，在试销过程中发现：每月销售量y（件）与销售单价x（x为正整数）（元）之间符合一次函数关系，当销售单价为55元时，月销售量为140件；当销售单价

为70元时，月销售量为80件．

（1）求y与x的函数关系式；

（2）如果每销售一件衬衫需支出各种费用1元，设服装店每月销售该种衬衫获利为w元，求w与x之间的函数关系式，并求出销售单价定为多少元时，商场获利最大，最大利润是多少元？

 

Answer 1

【答案】

解：（1）设y与x的函数关系式y=kx+b，由题意，得

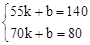，解得：。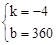

∴y与x的函数关系式为：y=﹣4x+360。

（2）由题意，得

W=y（x﹣40）﹣y=（﹣4x+360）（x﹣40）﹣（﹣4x+360）=﹣4x²+160x+360x﹣14400+4x﹣360

=﹣4x²+524x﹣14760，

∴w与x之间的函数关系式为：W=﹣4x²+524x﹣14760。

∵W=﹣4（x²﹣131x）﹣14760=﹣4（x﹣65.5）²+2401，

当x=65.5时，最大利润为2401元。

∵x为整数，∴x=66或65时，W=2400元。

∴x=65或66时，W_最大=2400元。

【解析】

试题分析：（1）设y与x的函数关系式y=kx+b，根据售价与销量之间的数量关系建立方程组，求出其解即可。

（2）根据利润=（售价﹣进价）×数量就可以表示出W，根据二次函数的性质求出最值。