
分析 (1)根据题意可以求得y与x的函数关系式,由供货商规定这种空气净化器售价不能低于600元/台,代理销售商每月要完成不低于60台的销售任务可以求得x的取值范围;
(2)根据题意可以得到w关于x的关系式,然后化为顶点式,从而可以求得w的最大值和此时x的值.
解答 解:(1)由题意可得,
y=50+(1000-x)÷20×5=300-$\frac{x}{4}$,
∵货商规定这种空气净化器售价不能低于600元/台,代理销售商每月要完成不低于60台的销售任务,
∴$\left\{\begin{array}{l}{x≥600}\\{300-\frac{x}{4}≥60}\end{array}\right.$,
解得,600≤x≤960,
即月销售量y(台)与售价x(元/台)之间的函数关系式是y=300-$\frac{x}{4}$(600≤x≤960);
(2)由题意可得,
w=(x-500)(300-$\frac{x}{4}$)=$-\frac{1}{4}(x-850)^{2}+30625$,
∴当x=850时,w取得最大值,此时w=30625,
即当售价x定为850元/台时,商场每月销售这种空气净化器所获得的利润w(元)最大,最大利润是30625元.
点评 本题考查二次函数的应用,解题的关键是明确题意,找出所求问题需要的条件.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:解答题
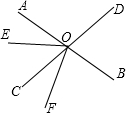 如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE:∠EOC=2:3.
如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE:∠EOC=2:3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com