
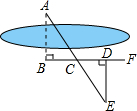
 如图所示,要测量河两岸上对岸两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再在BF的垂线DE上取点E,使A、C、E在同一条直线上,可以得到△ABC≌△EDC,得DE=AB,因此测得ED的长就是AB的长,判定△ABC≌△EDC的理由是( )
如图所示,要测量河两岸上对岸两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再在BF的垂线DE上取点E,使A、C、E在同一条直线上,可以得到△ABC≌△EDC,得DE=AB,因此测得ED的长就是AB的长,判定△ABC≌△EDC的理由是( )| A. | SSS | B. | ASA | C. | SAS | D. | HL |
科目:初中数学 来源: 题型:解答题
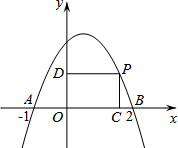 如图,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于点A(-1,0)和点B(2,0).点P是x轴上方抛物线上一动点(不落在y轴上),过点P作PD∥x轴交y轴于点D.PC∥y轴交x轴于点C,设点P的横坐标为m,矩形PDOC的周长为L.
如图,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于点A(-1,0)和点B(2,0).点P是x轴上方抛物线上一动点(不落在y轴上),过点P作PD∥x轴交y轴于点D.PC∥y轴交x轴于点C,设点P的横坐标为m,矩形PDOC的周长为L.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 打折前一次性购物总金额 | 优惠措施 |
| 不超过300元 | 不优惠 |
| 超过300元且不超过500元 | 售价一律打九折 |
| 超过500元 | 售价一律打八折 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com