
 =4,④x2=0,⑤x2-
=4,④x2=0,⑤x2- +3=0.
+3=0.科目:初中数学 来源: 题型:
| 1 | x+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
查看答案和解析>>
科目:初中数学 来源: 题型:
 “数形结合”是一种极其重要的思想方法.例如,我们可以利用数轴解分式不等式
“数形结合”是一种极其重要的思想方法.例如,我们可以利用数轴解分式不等式| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
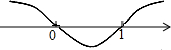 “数形结合”是一种极其重要的思想方法.例如,我们可以利用数轴解分式不等式
“数形结合”是一种极其重要的思想方法.例如,我们可以利用数轴解分式不等式 <1(x≠0).先考虑不等式的临界情况:方程
<1(x≠0).先考虑不等式的临界情况:方程 =1的解为x=1.如图,数轴上表示0和1的点将数轴“分割”成x<0、0<x<1和x>1三部分(0和1不算在内),依次考察三部分的数可得:当x<0和x>1时,
=1的解为x=1.如图,数轴上表示0和1的点将数轴“分割”成x<0、0<x<1和x>1三部分(0和1不算在内),依次考察三部分的数可得:当x<0和x>1时, <1成立.理解上述方法后,尝试运用“数形结合”的方法解决下列问题:
<1成立.理解上述方法后,尝试运用“数形结合”的方法解决下列问题: >1的解集是______;
>1的解集是______;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com