
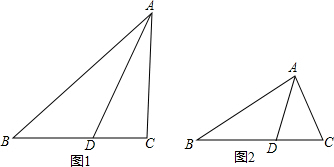
分析 (1)先构造全等三角形△ADE≌△ADC,得出结论再判断出△BDE是等腰三角形,转化即可;
(2)同(1)的方法,
(3)同(1)的方法,最后得出AB=CD-AC.
解答 解:(1)①如图1, 在AB上截取AE=AC,
在AB上截取AE=AC,
连接DE,
∵AD是∠BAC的平分线,
∴∠BAD=∠CAD
在△ADE和△ADC中,$\left\{\begin{array}{l}{AE=AC}\\{∠BAD=∠CAD}\\{AD=AD}\end{array}\right.$,
∴△ADE≌△ADC,
∴DE=DC,∠AED=∠C,
∵∠ACB=2∠B,
∴∠EBD=∠BDE,
∴BE=DE,
∴BE=DC,
∴AB=AE+BE=AC+CD;
②如图2,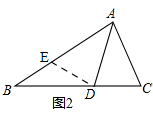 在AB上截取AE=AC,连接DE,
在AB上截取AE=AC,连接DE,
∵AD是∠BAC的平分线,
∴∠BAD=∠CAD
在△ADE和△ADC中,$\left\{\begin{array}{l}{AE=AC}\\{∠BAD=∠CAD}\\{AD=AD}\end{array}\right.$,
∴△ADE≌△ADC,
∴DE=DC,∠AED=∠ACB,
∵∠ACB=2∠B,
∴∠EBD=∠BDE,
∴BE=DE,
∴BE=DC,
∴AB=AE+BE=AC+CD;
(2)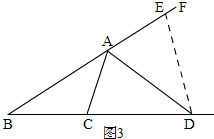
如图3,在BA的延长线AF上取一点E,使得AE=AC,连接DE
在△ADE和△ADC中,$\left\{\begin{array}{l}{AE=AC}\\{∠BAD=∠CAD}\\{AD=AD}\end{array}\right.$,
∴△ADE≌△ADC,
∴∠ACD=∠AED,CD=DE,
∴∠ACB=∠FED,
又∵∠ACB=2∠B,
∴∠FAD=2∠B,
又∵∠FED=∠B+∠EDB,
∴∠EDB=∠B,
∴DE=BE,
∴BE=CD,
∴AB=CD-AC.
点评 此题是三角形综合题,主要考查了角平分线的定义,全等三角形的判定和性质,用截长补短的方法是解本题的关键,本题也可以延长AC至G,使CG=CD.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 在某中学抽取200名女生 | |
| B. | 在某中学抽取200名男生 | |
| C. | 在某中学抽取200名学生 | |
| D. | 在河池市中学生中随机抽取200名学生 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2,3) | B. | (-3,2) | C. | (2,-3) | D. | (3,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,CD是⊙O的直径,AB是⊙O的弦,AB⊥CD,垂足为G,OG:OC=3:5,AB=8.
如图,CD是⊙O的直径,AB是⊙O的弦,AB⊥CD,垂足为G,OG:OC=3:5,AB=8.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. | 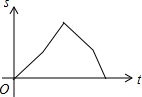 | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 随机抛掷一枚均匀的硬币,落地后反面一定朝上 | |
| B. | 从1、3、5、7、9中随机取一个数,取得的数不可能是偶数 | |
| C. | “彩票的中奖机会是1%”表示买100张彩票一定会中奖 | |
| D. | “明天降雨的概率是85%”表示明天有85%的时间降雨 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com