
 PD,求△POD与△PDG的面积之比;
PD,求△POD与△PDG的面积之比;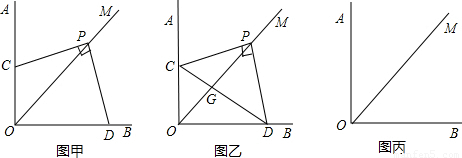
 解:(1)①证明:过P作PH⊥OA,PN⊥OB,垂足分别为H,N,得∠HPN=90°
解:(1)①证明:过P作PH⊥OA,PN⊥OB,垂足分别为H,N,得∠HPN=90° .
. (2)①若PC与边OA相交,
(2)①若PC与边OA相交, ED=OD=1
ED=OD=1

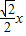 +x
+x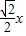 =
= +x
+x


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源:2003年全国中考数学试题汇编《二次函数》(04)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2003年浙江省绍兴市中考数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com