
·ÖĪö £Ø¢ń£©°ŃŗÆŹż½āĪöŹ½»ÆĪŖ¶„µćŹ½¼“æɵƵ½A£Ø1£¬$\sqrt{3}$£©£¬½ā·½³Ģ¼“æɵƵ½B£Ø2£¬0£©£»
£Ø¢ņ£©ÓÉy1=-$\sqrt{3}$x2+2$\sqrt{3}$xæŖæŚĻņĻĀ£¬¶„µć×ų±źĪŖA£Ø1£¬$\sqrt{3}$£©£¬ÓÉĪŽĀŪxČ”ŗĪĻąĶ¬ÖµŹ±£¬¶¼ÓŠy2£¾y1£¬µĆµ½Ö±Ļßy2=$\sqrt{3}$x+mÓėÅ×ĪļĻßy1=-$\sqrt{3}$x2+2$\sqrt{3}$xĪŽ½»µć£¬ÓŚŹĒµĆµ½”÷=£Ø$\sqrt{3}$£©2-4$\sqrt{3}$m£¼0£¬¼“æɲ»µČŹ½¼“æɵƵ½½įĀŪ£»
£Ø¢ó£©¢ŁČēĶ¼1ÖŠ£¬µ±k£¾1Ź±£¬Óė£Ø1£©Ķ¬ĄķæɵĆÅ×ĪļĻßC2µÄ½āĪöŹ½ĪŖy=-$\frac{\sqrt{3}}{k}$x2+2$\sqrt{3}$x¼°¶„µćCµÄ×ų±ź£¬øł¾ŻS”÷PAC=S”÷ABCÖŖBP”ĪAC£¬¼Ģ¶ųæɵƔ÷ABOŹĒ±ß³¤ĪŖ2µÄÕżČż½ĒŠĪ£¬ĖıߊĪCEBPŹĒ¾ŲŠĪ£¬±ķŹ¾³öµćPµÄ×ų±ź£¬½«Ęä“śČėµ½Å×ĪļĻßC2½āĪöŹ½æÉĒóµĆkµÄÖµ£»
¢ŚČēĶ¼2ÖŠ£¬µ±k£¼-1Ź±£¬×÷”÷ABO¹ŲÓŚyÖį¶Ō³ĘµÄ”÷A”äB”äO£¬OE”ä”ĶA”äB”䣬Ķ¬ĄķæɵĆĖıߊĪCEBPŹĒ¾ŲŠĪ£¬ĻČĒó³öÅ×ĪļĻßC2½āĪöŹ½£¬±ķŹ¾³öµćPµÄ×ų±ź£¬½«Ęä“śČėµ½Å×ĪļĻßC2½āĪöŹ½æÉĒóµĆkµÄÖµ£»
½ā“š ½ā£ŗ£Ø¢ń£©”ßy1=-$\sqrt{3}$x2+2$\sqrt{3}$x=-$\sqrt{3}$£Øx-1£©2+$\sqrt{3}$£¬
”ąA£Ø1£¬$\sqrt{3}$£©£¬
µ±y1=0Ź±£¬¼“-$\sqrt{3}$x2+2$\sqrt{3}$x=0£¬
”ąx1=0£¬x2=2£¬
”ąB£Ø2£¬0£©£»
£Ø¢ó£©”ßy1=-$\sqrt{3}$x2+2$\sqrt{3}$xæŖæŚĻņĻĀ£¬¶„µć×ų±źĪŖA£Ø1£¬$\sqrt{3}$£©£¬
”ßĪŽĀŪxČ”ŗĪĻąĶ¬ÖµŹ±£¬¶¼ÓŠy2£¾y1£¬
”ąÖ±Ļßy2=$\sqrt{3}$x+mÓėÅ×ĪļĻßy1=-$\sqrt{3}$x2+2$\sqrt{3}$xĪŽ½»µć£¬
¼“$\sqrt{3}$x+m=-$\sqrt{3}$x2+2$\sqrt{3}$xĪŽŹµŹżøł£¬
”ą”÷=£Ø$\sqrt{3}$£©2-4$\sqrt{3}$m£¼0£¬
”ąm£¾$\frac{\sqrt{3}}{4}$£¬
”ąmµÄ·¶Ī§ŹĒm£¾$\frac{\sqrt{3}}{4}$£®
£Ø¢ó£©¢ŁČēĶ¼1ÖŠ£¬µ±k£¾1Ź±£¬
”ßÅ×ĪļĻßC2¾¹żŌµćO£¬£Øk£¬$\sqrt{3}$k£©£¬£Ø2k£¬0£©Čżµć£¬
”ąÅ×ĪļĻßC2µÄ½āĪöŹ½ĪŖy=-$\frac{\sqrt{3}}{k}$x2+2$\sqrt{3}$x£¬
”ąO”¢A”¢CČżµć¹²Ļߣ¬ĒŅ¶„µćCĪŖ£Øk£¬$\sqrt{3}$k£©£¬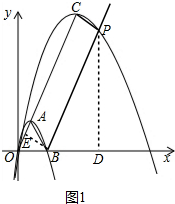
ČēĶ¼£¬”ßS”÷PAC=S”÷ABC£¬
”ąBP”ĪAC£¬
¹żµćP×÷PD”ĶxÖįÓŚD£¬¹żµćB×÷BE”ĶAOÓŚE£¬
ÓÉĢāŅāÖŖ”÷ABOŹĒ±ß³¤ĪŖ2µÄÕżČż½ĒŠĪ£¬ĖıߊĪCEBPŹĒ¾ŲŠĪ£¬
”ąOE=1£¬CE=BP=2k-1£¬
”ß”ĻPBD=60”ć£¬
”ąBD=k-$\frac{1}{2}$£¬PD=$\frac{\sqrt{3}}{2}$£Ø2k-1£©£¬
”ąP£Øk+$\frac{3}{2}$£¬$\frac{\sqrt{3}}{2}$£Ø2k-1£©£©£¬
”ą$\frac{\sqrt{3}}{2}$£Ø2k-1£©=-$\frac{\sqrt{3}}{2}$£Øk+$\frac{3}{2}$£©2+2$\sqrt{3}$£Øk+$\frac{3}{2}$£©£¬
½āµĆ£ŗk=$\frac{9}{2}$£»
¢ŚČēĶ¼2ÖŠ£¬µ±k£¼-1Ź±£¬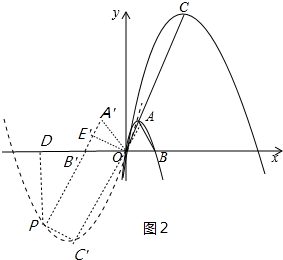
”ßÅ×ĪļĻßC2¾¹żŌµćO£¬£Øk£¬$\sqrt{3}$k£©£¬£Ø2k£¬0£©Čżµć£¬
”ąÅ×ĪļĻßC2µÄ½āĪöŹ½ĪŖy=-$\frac{\sqrt{3}}{k}$x2+2$\sqrt{3}$x£¬
”ąO”¢A”¢C”äČżµć¹²Ļߣ¬ĒŅ¶„µćC”äĪŖ£Øk£¬$\sqrt{3}$k£©£¬
×÷”÷ABO¹ŲÓŚyÖį¶Ō³ĘµÄ”÷A”äB”äO£¬OE”ä”ĶA”äB”䣬
”ßS”÷PAC”ä=S”÷ABC=S”÷AC”äB”䣬
”ąA”äP”ĪAC”䣬ÓÉĢāŅāĖıߊĪPC”äOE”äŹĒ¾ŲŠĪ£¬
”ąPE”ä=OC”ä=-2k£¬B”äE”ä=1£¬PB”ä=-2k-1£¬
ŌŚRt”÷PDB”äÖŠ£¬”ß”ĻPDB”ä=90”ć£¬”ĻPB”äD=”ĻA”äB”äO=60”ć£¬
”ąDB”ä=$\frac{1}{2}$PB”ä=$\frac{12k-1}{2}$£¬DP=$\frac{\sqrt{3}}{2}$£Ø-2k-1£©£¬
”ąµćP×ų±ź[$\frac{2k-3}{2}$£¬$\frac{\sqrt{3}}{2}$£Ø2k+1£©]£¬
”ą$\frac{\sqrt{3}}{2}$£Ø2k+1£©=-$\frac{\sqrt{3}}{k}$£Ø$\frac{2k-3}{2}$£©2+2$\sqrt{3}$£Ø$\frac{2k-3}{2}$£©
”ąk=-$\frac{9}{2}$£®
µćĘĄ ±¾ĢāÖ÷ŅŖæ¼²é“ż¶ØĻµŹżĒóŗÆŹż½āĪöŹ½¼°¶ž“ĪŗÆŹżµÄŠŌÖŹ”¢½āÖ±½ĒČż½ĒŠĪµČÖŖŹ¶µć£¬øł¾ŻĢāŅā±ķŹ¾³öµćPµÄ×ų±źŹĒ½āĢāµÄ¹Ų¼ü£¬Ń§»įĢķ¼ÓøØÖśĻß¹¹ŌģĢŲŹāĖıߊĪ½ā¾öĪŹĢā£¬ŹōÓŚÖŠæ¼Ń¹ÖįĢā£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
| ¹ŗʱČĖŹż | 1”«49ČĖ | 50”«100ČĖ | 100ČĖŅŌÉĻ |
| ĆæČĖĆÅʱ¼Ū | 130ŌŖ | 110ŌŖ | 90ŌŖ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
 ČēĶ¼£¬Õż·½ŠĪABCDÖŠ£¬AB=6£¬µćEŌŚ±ßCDÉĻ£¬ĒŅCE=2DE£®½«”÷ADEŃŲAE¶ŌÕŪÖĮ”÷AFE£¬ŃÓ³¤EF½»±ßBCÓŚµćG£¬Į¬½įAG”¢CF£®ĻĀĮŠ½įĀŪ£ŗ¢Ł”÷ABG”Õ”÷AFG£»¢ŚBG=GC£»¢ŪEG=DE+BG£»¢ÜAG”ĪCF£»¢ŻS”÷FGC=3.6£®ĘäÖŠÕżČ·½įĀŪŹĒ¢Ł¢Ś¢Ū¢Ü¢Ż£®
ČēĶ¼£¬Õż·½ŠĪABCDÖŠ£¬AB=6£¬µćEŌŚ±ßCDÉĻ£¬ĒŅCE=2DE£®½«”÷ADEŃŲAE¶ŌÕŪÖĮ”÷AFE£¬ŃÓ³¤EF½»±ßBCÓŚµćG£¬Į¬½įAG”¢CF£®ĻĀĮŠ½įĀŪ£ŗ¢Ł”÷ABG”Õ”÷AFG£»¢ŚBG=GC£»¢ŪEG=DE+BG£»¢ÜAG”ĪCF£»¢ŻS”÷FGC=3.6£®ĘäÖŠÕżČ·½įĀŪŹĒ¢Ł¢Ś¢Ū¢Ü¢Ż£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
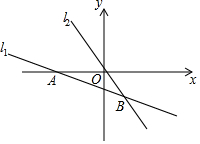 ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ö±Ļßl1£ŗy=-$\frac{1}{2}$x+bÓėÖ±Ļßl2£ŗy=kxĻą½»ÓŚµćB£Øm£¬-4£©£¬ĒŅÖ±Ļßl1ÓėxÖį½»ÓŚµćA£Ø-6£¬0£©£®
ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ö±Ļßl1£ŗy=-$\frac{1}{2}$x+bÓėÖ±Ļßl2£ŗy=kxĻą½»ÓŚµćB£Øm£¬-4£©£¬ĒŅÖ±Ļßl1ÓėxÖį½»ÓŚµćA£Ø-6£¬0£©£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
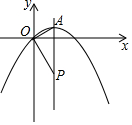 ŅŃÖŖ£ŗČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Å×ĪļĻßy=ax2+xµÄ¶Ō³ĘÖįĪŖÖ±Ļßx=2£¬¶„µćĪŖA£®µćPĪŖÅ×ĪļĻ߶Ō³ĘÖįÉĻŅ»µć£¬Į¬½įOA”¢OP£®µ±OA”ĶOPŹ±£¬Pµć×ų±źĪŖ£Ø2£¬-4£©£®
ŅŃÖŖ£ŗČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Å×ĪļĻßy=ax2+xµÄ¶Ō³ĘÖįĪŖÖ±Ļßx=2£¬¶„µćĪŖA£®µćPĪŖÅ×ĪļĻ߶Ō³ĘÖįÉĻŅ»µć£¬Į¬½įOA”¢OP£®µ±OA”ĶOPŹ±£¬Pµć×ų±źĪŖ£Ø2£¬-4£©£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
| Į“Ģõ½ŚŹż£Ø½Ś£© | 2 | 3 | 4 |
| Į“Ģõ³¤¶Č£Øcm£© | 4.2 | 5.9 | 7.6 |

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | -2 | B£® | 1 | C£® | 0 | D£® | 3 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
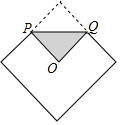 ½«±ß³¤ĪŖ1µÄÕż·½ŠĪ½ķµÄŅ»½ĒÕŪµžÖĮÕż·½ŠĪµÄÖŠŠÄĪ»ÖĆ£¬ÕŪŗŪPQµÄ³¤ĪŖ£Ø””””£©
½«±ß³¤ĪŖ1µÄÕż·½ŠĪ½ķµÄŅ»½ĒÕŪµžÖĮÕż·½ŠĪµÄÖŠŠÄĪ»ÖĆ£¬ÕŪŗŪPQµÄ³¤ĪŖ£Ø””””£©| A£® | 1 | B£® | 2 | C£® | $\frac{\sqrt{2}}{2}$ | D£® | $\sqrt{2}$ |
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com