
【题目】2018年某市高中招生体育考试规定:九年级男生考试项目有A、B、C、D、E五类:其中A:1000米跑![]() 必考项目
必考项目![]() ;B:跳绳;C:引体向上;D:立定跳远;E:50米跑,再从B、C、D、E中各选两项进行考试.
;B:跳绳;C:引体向上;D:立定跳远;E:50米跑,再从B、C、D、E中各选两项进行考试.
![]() 若男生甲第一次选一项,直接写出男生甲选中项目E的概率.
若男生甲第一次选一项,直接写出男生甲选中项目E的概率.
![]() 若甲、乙两名九年级男生在选项的过程中,第一次都是选了项目E,那么他俩第二次同时选择跳绳或立定跳远的概率是多少?请用列表法或画树状图的方法加以说明并列出所有等可能的结果.
若甲、乙两名九年级男生在选项的过程中,第一次都是选了项目E,那么他俩第二次同时选择跳绳或立定跳远的概率是多少?请用列表法或画树状图的方法加以说明并列出所有等可能的结果.
科目:初中数学 来源: 题型:
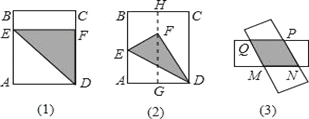
【题目】在一张长方形纸片ABCD中,AB=25cm,AD=20cm,现将这张纸片按下列图示方法折叠,请解决下列问题.
(1)如图(1),折痕为DE,点A的对应点F在CD上,求折痕DE的长;
(2)如图(2),H,G分别为BC,AD的中点,A的对应点F在HG上,折痕为DE,求重叠部分的面积;
(3)如图(3),在图(2)中,把长方形ABCD沿着HG对开,变成两张长方形纸片,按图示方式将两张纸片任意叠合后,判断重叠四边形的形状,并证明;
(4)在(3)中,重叠四边形的周长是否存在最大值或最小值?如果存在,试求出来;如果不存在,试简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图像与正比例函数
的图像与正比例函数![]() 的图像都经过点
的图像都经过点![]() ,点
,点![]() 在反比例函数
在反比例函数![]() 的图像上,点
的图像上,点![]() 在正比例函数
在正比例函数![]() 的图像上.
的图像上.
(1)求此正比例函数的解析式;
(2)求线段AB的长;
(3)求△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
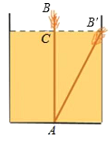
【题目】"引葭赴岸“是《九章算木》中的- -道題:”今有池一丈 ,葭生其中央,出水一尺,引葭赴岸,迺与岸芥.伺水深,葭氏各几何?"題意是:有一个边长为10尺的正方形池塘,一棵芦苇AB生长在它的中央,高出水面BC为1尺.如果把该芦苓沿与水池边垂直的方向拉向岸辺,那么芦革的顶部B恰好碰到岸边的B'. 向芦苇长多少? (画出几何图形并解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,![]() 中,
中,![]() .
.

(1)按要求作出图形:
①延长![]() 到点
到点![]() ,使
,使![]() ;②延长
;②延长![]() 到点
到点![]() ,使
,使![]() ;③连接
;③连接![]() ,
,![]() .
.
(2)猜想(1)中线段![]() 与
与![]() 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
解:(1)完成作图
(2)![]() 与
与![]() 的大小关系是______
的大小关系是______
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将ABCD的AD边延长至点E,使DE=![]() AD,连接CE,F是BC边的中点,连接FD.
AD,连接CE,F是BC边的中点,连接FD.
(1)求证:四边形CEDF是平行四边形;
(2)若AB=3,AD=4,∠A=60°,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数![]() 、
、![]() 、
、![]() 都是常数,且
都是常数,且![]() 叫做“奇特函数”,当
叫做“奇特函数”,当![]() 时,奇特函数
时,奇特函数![]() 就成为反比例函数
就成为反比例函数![]() 是常数,且
是常数,且![]() .
.
![]() 若矩形的两边长分别是
若矩形的两边长分别是![]() 、
、![]() ,当两边长分别增加
,当两边长分别增加![]() 、
、![]() 后得到的新矩形的面积是
后得到的新矩形的面积是![]() ,求
,求![]() 与
与![]() 的函数关系式,并判断这个函数是否“奇特函数”;
的函数关系式,并判断这个函数是否“奇特函数”;
![]() 如图在直角坐标系中,点
如图在直角坐标系中,点![]() 为原点矩形
为原点矩形![]() 的顶点,
的顶点,![]() 、
、![]() 坐标分别为
坐标分别为![]() 、
、![]() ,点
,点![]() 是
是![]() 中点,连接
中点,连接![]() 、
、![]() 交于
交于![]() ,“奇特函数”
,“奇特函数”![]() 的图象经过点
的图象经过点![]() 、
、![]() ,求这个函数的解析式,并判断
,求这个函数的解析式,并判断![]() 、
、![]() 、
、![]() 三点是否在这个函数图象上;
三点是否在这个函数图象上;
![]() 对于
对于![]() 中的“奇特函数”
中的“奇特函数”![]() 的图象,能否经过适当的变换后与一个反比例函数图象重合,若能,请直接写出具体的变换过程和这个反比例函数解析式;若不能,请简述理由.
的图象,能否经过适当的变换后与一个反比例函数图象重合,若能,请直接写出具体的变换过程和这个反比例函数解析式;若不能,请简述理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
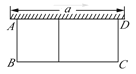
【题目】如图,有一个长为24米的篱笆,一面利用墙(墙的最大长度a为15米)围成的中间隔有一道篱笆的长方形花圃.设花圃的宽AB为x米,面积为S平方米.
(1)求S与x的函数关系式;
(2)如果要使围成花圃面积最大,求AB的长为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习完第十二章后,张老师让同学们独立完成课本56页第9题:“如图1,![]() ,
,![]() ,
,![]() ,
,![]() ,垂足分别为
,垂足分别为![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.”
的长.”

(1)请你也独立完成这道题:
(2)待同学们完成这道题后,张老师又出示了一道题:
在课本原题其它条件不变的前提下,将![]() 所在直线旋转到
所在直线旋转到![]() 的外部(如图2),请你猜想
的外部(如图2),请你猜想![]() ,
,![]() ,
,![]() 三者之间的数量关系,直接写出结论:_______.(不需证明)
三者之间的数量关系,直接写出结论:_______.(不需证明)
(3)如图3,将(1)中的条件改为:在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 三点在同一条直线上,并且有∠BEC=∠ADC=∠BCA=
三点在同一条直线上,并且有∠BEC=∠ADC=∠BCA=![]() ,其中
,其中![]() 为任意钝角,那么(2)中你的猜想是否还成立?若成立,请证明;若不成立,请说明理由:
为任意钝角,那么(2)中你的猜想是否还成立?若成立,请证明;若不成立,请说明理由:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com