练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．已知△ABC中，BC=6，AB、AC的垂直平分线分别交边BC于点M、N，若MN=2，则△AMN的周长是（　　）
    A．4B．6C．4或8D．6或10

    分析 由直线PM为线段AB的垂直平分线，根据线段垂直平分线定理：线段垂直平分线上的点到线段两端点的距离相等可得AM=BM，同理可得AN=NC，然后表示出三角形AMN的三边之和，等量代换可得其周长等于BC的长，由BC的长即可得到三角形AMN的周长．

    解答 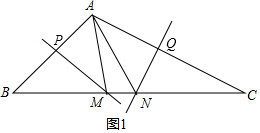解：图1，∵直线MP为线段AB的垂直平分线，
    ∴MA=MB，
    又直线NQ为线段AC的垂直平分线，
    ∴NA=NC，
    ∴△AMN的周长l=AM+MN+AN=BM+MN+NC=BC，
    又BC=6，
    则△AMN的周长为6，
    如图2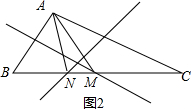，△AMN的周长l=AM+MN+AN=BM+MN+NC=BC+2MN，
    又BC=6，
    则△AMN的周长为10，
    故选D．

    点评 此题考查了线段垂直平分线定理的运用，利用了转化的思想，熟练掌握线段垂直平分线定理是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    4．有理数a、b在数轴上的位置如图所示，那么下列式子中成立的是（　　）
    A．a＞bB．a＜bC．ab＞0D．$\frac{a}{b}$＞0

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．有理数a、b、c在数轴上的位置如图所示：若m=|a+b|-|b-1|-|a-c|-|1-c|，则1000m的值是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

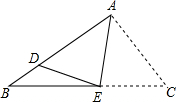    2．如图，△ABC中，∠ABC=30°，∠ACB=50°，折叠△ACB使点C与AB边上的点D重合，折痕为AE，连DE，则∠AED为（　　）
    A．70°B．75°C．80°D．85°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．下列各式运算正确的是（　　）
    A．a2+b3=a5B．a2•b3=a6C．（ab2）3=ab6D．a10÷a2=a8

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．抛物线y=（x-1）2-2向右平移1个单位长度，再向上平移1个单位长度，此时抛物线的顶点为（　　）
    A．（1，3）B．（2，-1）C．（0，-1）D．（0，1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．已知：已知二次函数的图象与x轴交于A（-3，0）和B（1，0）两点．交y轴于点C（0，3），点C，D是二次函数图象上的一对对称点，一次函数的图象过点B，D
    （1）画出图象，并求二次函数的解析式．
    （2）根据图象直接写出使一次函数值大于或等于二次函数值的x的取值范围．
    （3）若直线与y轴交点为E，连接AD，AE，求三角形ADE的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．下列调查中，最适合采用抽样调查（抽查）的是（　　）
    A．调查“神州十一号飞船”各部分零件情况
    B．调查旅客随身携带的违禁物品
    C．调查全国高中学生对“数学核心素养”的了解
    D．调查某校九年级（1）班学生中考体育成绩

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

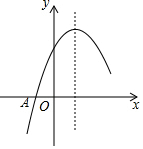    4．如图是二次函数y=ax2+bx+c图象的一部分，图象过点A（-1，0），对称轴为直线x=1，给出以下结论：
    ①abc＜0；②b2-4ac＞0；③9a+3b+c＞0；④若B（$\frac{1}{2}$，y1）、C（2，y2）为函数图象上的两点，则y1＞y2，
    其中正确的结论是（填写代表正确结论的序号）①②④．

    查看答案和解析>>

    同步练习册答案