
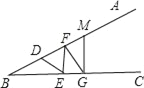
【题目】已知:如图,BD=DE=EF=FG.
(1)若∠ABC=20°,∠ABC内符合条件BD=DE=EF=FG的折线(如DE、EF、FG)共有几条?若∠ABC=10°呢?试一试,并简述理由.
(2)若∠ABC=m°(0<m<90),你能找出一个折线条数n与m之间的关系吗?若有,请找出来;若无,请说明理由.
【答案】(1)有4条,若∠ABC=10°,有8条;(2)n<![]() 的整数.
的整数.
【解析】
(1)根据已知可得到几组相等的角,再根据三角形外角的性质可得到∠EDF、∠FEG、∠AFG、∠AMG分别与∠B的关系,再根据三角形内角和定理即可求解.
(2)结合第(1)题,根据三角形内角和定理可知,需满足mn<90°,从而不难求解.
(1)有4条,若∠ABC=10°,有8条.
当∠ABC=20°,
∵BD=DE=EF=FG=GM,
∴∠DEB=∠B,∠EDF=∠EFD,∠FEG=∠FGE,∠GFM=∠FMG
∵∠EDF=2∠B=40°,∠FEG=3∠B=60°,∠AFG=4∠B=80°,∠AMG=5∠B=100°,
∴同理:∠AMG将成为下一个等腰三角形的底角
∵100°+100°>180°
∴不会再由下一条折线
∴共有四条拆线,分别是:DE、EF、FG,GM.
同理:当∠ABC=10°,有8条符合条件的折线.
(2)由(1)可知∠EDF=2∠B=2m°,∠FEG=3∠B=3m°,∠AFG=4∠B=4m°,
∵根据三角形内角和定理可知,需满足mn<90°,
∴n<![]() 的整数.
的整数.


 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,则在下列条件:①∠C=∠D ②AC=AD ③∠CBA=∠DBA ④BC=BD中任选一个能判定△ABC≌△ABD的是( )
,则在下列条件:①∠C=∠D ②AC=AD ③∠CBA=∠DBA ④BC=BD中任选一个能判定△ABC≌△ABD的是( )

A. ①②③④ B. ②③④ C. ①③④ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列判断正确的是( )
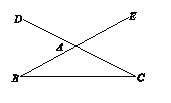
A. 有2对同位角,2对内错角,2对同旁内角
B. 有2对同位角,2对内错角,3对同旁内角
C. 有4对同位角,2对内错角,4对同旁内角
D. 以上判断均不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在四边形![]() 中,∠A=∠C=90°.
中,∠A=∠C=90°.
(1)如图1,若BE平分∠ABC,DF平分∠ADC的邻补角,请写出BE与DF的位置关系,并证明.

(2)如图2,若BF、DE分别平分∠ABC、∠ADC的邻补角,判断DE与BF位置关系并证明.

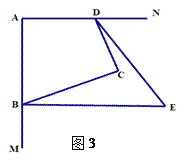
(3)如图3,若BE、DE分别五等分∠ABC、∠ADC的邻补角(即∠CDE=![]() ,∠CBE=
,∠CBE=![]() ),则∠E= .
),则∠E= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行于y轴的直尺(一部分)与双曲线y= ![]() (k≠0)(x>0)相交于点A、C,与x轴相交于点B、D,连接AC.已知点A、B的刻度分别为5,2(单位:cm),直尺的宽度为2cm,OB=2cm.
(k≠0)(x>0)相交于点A、C,与x轴相交于点B、D,连接AC.已知点A、B的刻度分别为5,2(单位:cm),直尺的宽度为2cm,OB=2cm.
(1)求k的值;
(2)求经过A、C两点的直线的解析式;
(3)连接OA、OC,求△OAC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形都是由同样大小的正方形按照一定规律所组成的,其中第①个图形中一个有2个正方形,第②个图形中一共有8个正方形,第③个图形中一共有16个正方形,…,按此规律,第⑦个图形中正方形的个数为( )

A. 56 B. 65 C. 68 D. 71
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、B、C、D、E在同一直线上,且AC=BD,E是线段BC的中点.
![]()
(1)点E是线段AD的中点吗?说明理由;
(2)当AD=10,AB=3时,求线段BE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD是经过∠BCA的顶点C的一条直线,CA=CB,E,F是直线CD上的两点,且∠BEC=∠CFA=α.
(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:
①如图(a),若∠BCA=90°,α=90°,则BE________CF,EF________|BE-AF|(填“>”“<”或“=”);
②如图(b),若0°<∠BCA<180°,请添加一个关于α与∠BCA关系的条件________,使①中的两个结论仍然成立,并证明两个结论成立;
(2)如图(c),若直线CD经过∠BCA的外部,∠BCA=α,请写出EF,BE,AF三条线段数量关系的合理猜想(不要求证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并解决有关问题:
我们知道, ,现在我们可以用这一结论来化简含有绝对值的式子,例如化简式子
,现在我们可以用这一结论来化简含有绝对值的式子,例如化简式子![]() 时,可令
时,可令![]() 和
和![]() ,分别求得
,分别求得![]() ,
,![]() (称
(称![]() 、
、![]() 分别为
分别为![]() 与
与![]() 的零点值)。在有理数范围内,零点值
的零点值)。在有理数范围内,零点值![]() 和
和![]() 可将全体有理数不重复且不遗漏地分成如下三种情况:(1)
可将全体有理数不重复且不遗漏地分成如下三种情况:(1)![]() ;(2)
;(2)![]() ≤
≤![]() ;(3)
;(3)![]() ≥2。从而化简代数式
≥2。从而化简代数式![]() 可分为以下3种情况:
可分为以下3种情况:
(1)当![]() 时,原式
时,原式![]() ;
;
(2)当![]() ≤
≤![]() 时,原式
时,原式![]() ;
;
(3)当![]() ≥2时,原式
≥2时,原式![]()
综上所述:原式
通过以上阅读,请你类比解决以下问题:
(1)填空:![]() 与
与![]() 的零点值分别为 ;
的零点值分别为 ;
(2)化简式子![]() 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com