

分析 (1)利用△AED≌△BFA求得AE=BF,再利用线段关系求出AF-BF=EF;
(2)由AG=$\sqrt{5}$BG,设BG=t,则AG=$\sqrt{5}$t,在Rt△ABG中,AB=$\sqrt{{AG}^{2}{-BG}^{2}}$=2t,得到BC=2t,由△ABG∽△AED,得到$\frac{AG}{AD}$=$\frac{BG}{AE}$,求出AE=$\frac{2\sqrt{5}}{5}$t,EG=$\frac{3\sqrt{5}}{5}$t,于是得到GC:EG=t:$\frac{3\sqrt{5}}{5}$t=$\frac{\sqrt{5}}{3}$;
(3)连接DG,作EM⊥BC于M点,利用直角三角形求出DG,CD的长,再利用ABG∽△DEA,求出AD,再运用△EMG∽△DEA求出EM和MG,再运用勾股定理即可求出CE的长.
解答 (1)证明:∵四边形ABCD为矩形,AB=BC,
∴四边形ABCD为正方形,
∴AD=AB,∠BAD=90°,
又∵DE⊥AG,BF∥DE,
∴∠AED=∠AFB=90°,
∵∠BAF+∠DAE=90°,∠BAE+∠ABF=90°,
∴∠DAE=∠ABF,
在△AED和△BFA中,
$\left\{\begin{array}{l}{∠AED=∠AFB}\\{∠DAE=∠ABF}\\{AD=AB}\end{array}\right.$
∴△AED≌△BFA(AAS),
∴AE=BF,
∴AF-BF=EF,
(2)解:∵AG=$\sqrt{5}$BG,
设BG=t,则AG=$\sqrt{5}$t,
在Rt△ABG中,AB=$\sqrt{{AG}^{2}{-BG}^{2}}$=2t,
∴BC=2t,
∵∠BAD+∠GAD=∠BAD+∠AGB=90°,
∴∠GAD=∠AGB,
∵∠ABC=∠AED=90°,
∴△ABG∽△AED,
∴$\frac{AG}{AD}$=$\frac{BG}{AE}$,
∴AE=$\frac{2\sqrt{5}}{5}$t,
∴EG=$\frac{3\sqrt{5}}{5}$t,
∴GC:EG=t:$\frac{3\sqrt{5}}{5}$t=$\frac{\sqrt{5}}{3}$;
(3)解:如图3,连接DG,作EM⊥BC于M点,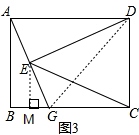 ∵DE⊥AG,DE=2,GE=1,
∵DE⊥AG,DE=2,GE=1,
∴在RT△DEG中,DG=$\sqrt{{DE}^{2}{+GE}^{2}}$=$\sqrt{{2}^{2}{+1}^{2}}$=$\sqrt{5}$,
∵CG=CD,
∴在RT△DCG中,∠CDG=∠CGD=45°,
∴CD=CG=$\frac{DG}{\sqrt{2}}$=$\frac{\sqrt{10}}{2}$,
∵∠BAG+∠GAD=90°,∠EDA+∠GAD=90°,
∴∠BAG=∠EDA,
∵∠ABG=∠DEA=90°,
∴△ABG∽△DEA,
∴$\frac{AD}{AG}$=$\frac{DE}{AB}$,
设AD=x,则AE=$\sqrt{{x}^{2}{-DE}^{2}}$=$\sqrt{{x}^{2}-4}$,AG=$\sqrt{{x}^{2}-4}$+1,
∴$\frac{x}{\sqrt{{x}^{2}-4}+1}$=$\frac{2}{\frac{\sqrt{10}}{2}}$,
解得x1=$\frac{2\sqrt{10}}{3}$,x2=-2$\sqrt{10}$(舍去)
∴AE=$\sqrt{{AD}^{2}{-DE}^{2}}$=$\frac{2}{3}$,
又∵∠BAG=∠MEG,
∴∠EDA=∠MEG,
∴△EMG∽△DEA
∴$\frac{GE}{AD}$=$\frac{EM}{DE}$=$\frac{MG}{AE}$,即$\frac{1}{\frac{2\sqrt{10}}{3}}$=$\frac{EM}{2}$=$\frac{MG}{\frac{2}{3}}$,
解得EM=$\frac{3\sqrt{10}}{10}$,MG=$\frac{\sqrt{10}}{10}$,
∴CM=CG+MG=$\frac{\sqrt{10}}{2}$+$\frac{\sqrt{10}}{10}$=$\frac{3\sqrt{10}}{5}$,
∴CE=$\sqrt{{EM}^{2}{+CE}^{2}}$=$\sqrt{{(\frac{3\sqrt{10}}{10})}^{2}{+(\frac{3\sqrt{10}}{5})}^{2}}$=$\frac{3\sqrt{2}}{2}$.
故答案为:$\frac{3\sqrt{2}}{2}$.
点评 本题主要考查了矩形的性质,全等三角形的判定与性质,相似三角形的判定和性质,勾股定理,解题的关键是正确作出辅助线,运用三角形相似求出线段的长度.此题难度较大,考查了学生计算能力.解题时一定要细心.


科目:初中数学 来源: 题型:填空题
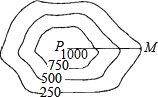 测量队为了测量某地区山顶P的海拔,选择M点作为观测点,从M点测得山顶P的仰角为30°,在比例尺为1:50000的该地区等高线地形图上,量得这两点间的图上距离为3cm,则山顶P的海拔为1116m.($\sqrt{3}$≈1.732)
测量队为了测量某地区山顶P的海拔,选择M点作为观测点,从M点测得山顶P的仰角为30°,在比例尺为1:50000的该地区等高线地形图上,量得这两点间的图上距离为3cm,则山顶P的海拔为1116m.($\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com