
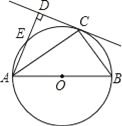
【题目】如图,C为以AB为直径的⊙O上一点,AD和过点C的切线互相垂直,垂足为点D.
(1)求证:AC平分∠BAD;
(2)若CD=3,AC=3![]() ,求⊙O的半径长.
,求⊙O的半径长.
【答案】(1)证明:连结OC(如图所示)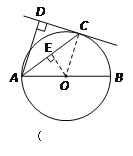
则∠ACO=∠CAO (等腰三角形,两底角相等)
∵CD切⊙O于C,∴CO⊥CD.
又∵AD⊥CD
∴AD∥CO
∴∠DAC=∠ACO (两直线平行,内错角相等)
∴∠DAC=∠CAO
∴AC平分∠BAD ----------------5分
(2)过点E画OE⊥AC于E(如图所示)
在Rt△ADC中,AD=![]() =6
=6
∵OE⊥AC, ∴AE=![]() AC=
AC=![]()
∵ ∠CAO=∠DAC,∠AEO=∠ADC=Rt∠
∴△AEO∽△ADC
∴![]() 即
即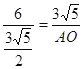
∴AO=![]() 即⊙O的半径为
即⊙O的半径为![]() . ----------------5分
. ----------------5分
【解析】
试题(1)首先连接OC,由CD切⊙O于C,根据切线的性质,可得OC⊥CD,又由AD⊥CD,可得OC∥AD,又由OA=OC,易证得∠DAC=∠CAO,即AC平分∠BAD;
(2)首先过点O作OE⊥AC于E,由CD=3,AC=3![]() ,在Rt△ADC中,利用勾股定理即可求得AD的长,由垂径定理,即可得AE的长,然后易证得△AEO∽△ADC,根据相似三角形的对应边成比例,即可求得⊙O的半径长.
,在Rt△ADC中,利用勾股定理即可求得AD的长,由垂径定理,即可得AE的长,然后易证得△AEO∽△ADC,根据相似三角形的对应边成比例,即可求得⊙O的半径长.
试题解析:(1)证明:连接OC,
∵OA=OC,
∴∠ACO=∠CAO,
∵CD切⊙O于C,
∴CO⊥CD.
又∵AD⊥CD,
∴AD∥CO,
∴∠DAC=∠ACO,
∴∠DAC=∠CAO,
∴AC平分∠BAD;
(2)解:过点O作OE⊥AC于E,
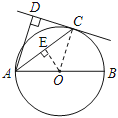
∵CD=3,AC=3![]() ,
,
在Rt△ADC中,AD=![]() ,
,
∵OE⊥AC,
∴AE=![]() AC=
AC=![]() ,
,
∵∠CAO=∠DAC,∠AEO=∠ADC=90°,
∴△AEO∽△ADC,
∴![]() ,
,
即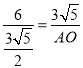 ,
,
∴AO=![]() ,
,
即⊙O的半径为![]() .
.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
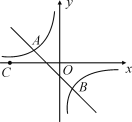
【题目】如图,点A(-2,n),B(1,-2)是一次函数y=kx+b的图象和反比例函数y=![]() 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出,当kx+b<![]() 时,x的取值范围;
时,x的取值范围;
(3)若C是x轴上一动点,设t=CB-CA,求t的最大值,并求出此时点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
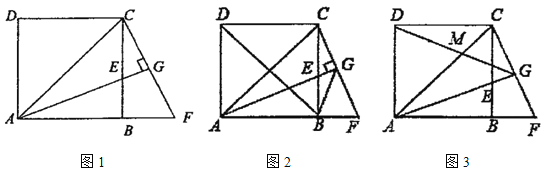
【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过边长为3的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,在正方形
,在正方形![]() 中,
中,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,
,
(1)求证:![]() ;
;
(2)如图![]() ,连接
,连接![]() 、
、![]() ,求证
,求证![]() 平分
平分![]() ;
;
(3)如图![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() , 求
, 求![]() 的值。
的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
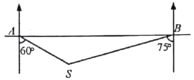
【题目】一艘轮船在![]() 处测得灯塔
处测得灯塔![]() 在船的南偏东60°方向,轮船继续向正东航行30海里后到达
在船的南偏东60°方向,轮船继续向正东航行30海里后到达![]() 处,这时测得灯塔
处,这时测得灯塔![]() 在船的南偏西75°方向,则灯塔
在船的南偏西75°方向,则灯塔![]() 离观测点
离观测点![]() 、
、![]() 的距离分别是( )
的距离分别是( )
A.![]() 海里、15海里B.
海里、15海里B.![]() 海里、15海里
海里、15海里
C.![]() 海里、
海里、![]() 海里D.
海里D.![]() 海里、
海里、![]() 海里
海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两种客车,2辆甲种客车与3辆乙种客车的总载客量为180人,1辆甲种客车与2辆乙种客车的总载客量为105人.
(1)请问1辆甲种客车与1辆乙种客车的载客量分别为多少人?
(2)某学校组织240名师生集体外出活动,拟租用甲、乙两种客车共6辆,一次将全部师生送到指定地点.若每辆甲种客车的租金为400元,每辆乙种客车的租金为280元,请给出最节省费用的租车方案,并求出最低费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com