
分析 (1)利用题意列方程5x2+3=4x2+4x,然后利用因式分解法解方程即可;
(2)利用求差法得到M-N=(x-1)(x-3),然后根据x的取值范围确定积的符合,从而得到M与N的关系关系.
解答 解:(1)根据题意得5x2+3=4x2+4x,
整理得x2-4x+3=0,
(x-1)(x-3)=0,
x-1=0或x-3=0,
所以x1=1,x2=3;
(2)M-N=5x2+3-(x2+4x)=x2-4x+3=(x-1)(x-3),
∵1<x<$\frac{5}{2}$,
∴x-1>0,x-3<0,
∴M-N=(x-1)(x-3)<0,
∴M<N.
点评 本题考查了解一元二次方程-因式分解法:因式分解法就是利用因式分解求出方程的解的方法,这种方法简便易用,是解一元二次方程最常用的方法.注意因式分解的应用.


科目:初中数学 来源: 题型:解答题
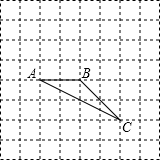 如图在8×8的正方形网格中,△ABC的顶点在边长为1的小正方形的顶点上.
如图在8×8的正方形网格中,△ABC的顶点在边长为1的小正方形的顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是“赵爽弦图”,其中△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,根据这个图形的面积关系,可以证明勾股定理.设AD=c,AE=a,DE=b,取c=10,a-b=2.
如图是“赵爽弦图”,其中△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,根据这个图形的面积关系,可以证明勾股定理.设AD=c,AE=a,DE=b,取c=10,a-b=2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
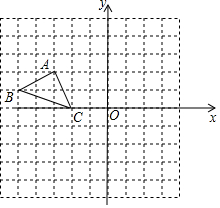 在平面直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(-3,2).
在平面直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(-3,2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
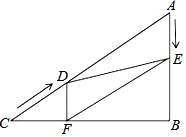 如图,在Rt△ABC中,∠B=90°,AC=120cm,∠A=60°,点D从点C出发沿
如图,在Rt△ABC中,∠B=90°,AC=120cm,∠A=60°,点D从点C出发沿| A. | 20秒 | B. | 18秒 | C. | 12秒 | D. | 6秒 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | -1 | C. | 1 | D. | 2016 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)已知x+y=4,x2+y2=9,求xy的值;
(1)已知x+y=4,x2+y2=9,求xy的值;查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{5}$=$\sqrt{7}$ | B. | $\sqrt{(-2)^{2}}$=-2 | C. | ($\sqrt{-2}$)2=2 | D. | 2÷$\sqrt{2}$=$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
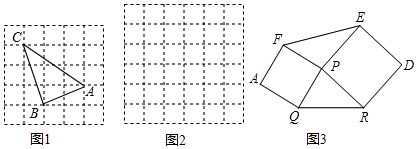
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com