
已知关于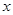 的一元二次方程
的一元二次方程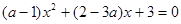 .
.
(1)求证:当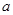 取不等于l的实数时,此方程总有两个实数根.
取不等于l的实数时,此方程总有两个实数根.
(2)若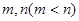 是此方程的两根,并且
是此方程的两根,并且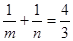 ,直线
,直线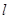 :
: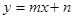 交
交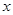 轴于点A,交
轴于点A,交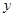 轴于点B,坐标原点O关于直线
轴于点B,坐标原点O关于直线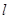 的对称点O′在反比例函数
的对称点O′在反比例函数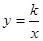 的图象上,求反比例函数
的图象上,求反比例函数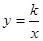 的解析式.
的解析式.
(3)在(2)的成立的条件下,将直线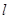 绕点A逆时针旋转角
绕点A逆时针旋转角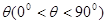 ,得到直线
,得到直线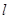 ′,
′,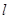 ′交
′交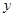 轴于点P,过点P作
轴于点P,过点P作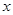 轴的平行线,与上述反比例函数
轴的平行线,与上述反比例函数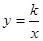 的图象交于点Q,当四边形APQO′的面积为
的图象交于点Q,当四边形APQO′的面积为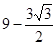 时,求角
时,求角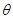 的值.
的值.
(1)证明
∵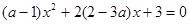 为关于
为关于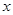 的一元二次方程
的一元二次方程
∴ ,即
,即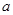 ≠1
≠1
∴△=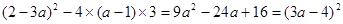
∴△≥0
∴当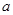 取不等于1的实数时,此方程总有两个实数根.
取不等于1的实数时,此方程总有两个实数根.
∴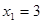 ,
,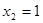
(2)∵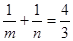
∴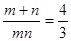
又∵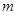 、
、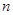 是方程
是方程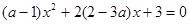 的两根
的两根
∴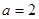
∵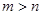
∴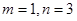
∴直线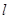 的解析式为
的解析式为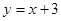
∴直线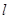 与
与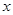 轴交点A(-3,0)与
轴交点A(-3,0)与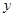 轴交点B(0,3)
轴交点B(0,3)
∴△ABO为等腰直角三角形
∴坐标原点O关于直线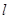 的对称点O′的坐标为(-3,3)
的对称点O′的坐标为(-3,3)
∴反比例函数的解析式为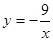
(3)解:设点P的坐标为(0,P),延长PQ和AO′交于点G
∵PQ∥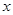 轴,与反比例函数图象交于点Q
轴,与反比例函数图象交于点Q
∴四边形AOPG为矩形
∴Q的坐标为(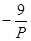 ,P)
,P)
∴G(-3,P)
当0°<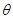 <45°,即P>3时
<45°,即P>3时
∵GP=3,GQ=3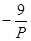 ,GO′=P-3,GA=P
,GO′=P-3,GA=P
∴S四边形APQO’=S△APG-S△GQO’
=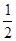 ×GA×GP-
×GA×GP-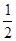 ×GQ×GO’
×GQ×GO’
=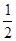 ×P×3-
×P×3-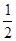 (3
(3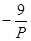 )×(P-3)
)×(P-3)
=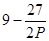
∴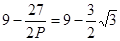
∴P=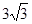
经检验,P=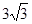 符合题意
符合题意
∴P(0,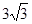 )
)
∴AP=6
点A关于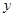 轴的对称点A′(3,0),连结A′P,
轴的对称点A′(3,0),连结A′P,
易得AP=PA′=6,又∵AA′=6
∴AA′=AP=A′P
∴∠PAO=60°
∵∠BAO=45°
∴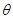 =∠PAO -∠BAO =60°-45°=15°
=∠PAO -∠BAO =60°-45°=15°
当45°≤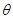 <90°,即P<-3时,
<90°,即P<-3时,
可类似地求得P=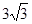 ,这与P<-3矛盾,所以此时点P不存在
,这与P<-3矛盾,所以此时点P不存在
∴旋转角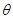 =15°
=15°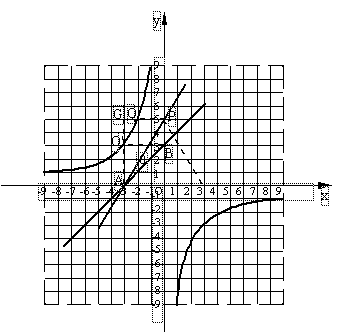
解析


科目:初中数学 来源: 题型:
| 8 |
查看答案和解析>>
科目:初中数学 来源:2013-2014学年广东省九年级上学期期末考试数学试卷(解析版) 题型:计算题
已知关于 的一元二次方程x2+2x+m=0.
的一元二次方程x2+2x+m=0.
(1)当m=3时,判断方程的根的情况;
(2)当m=-3时,求方程的根.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省宜城市九年级第一学期期中测试数学试卷(解析版) 题型:解答题
已知关于 的一元二次方程
的一元二次方程 有两个不相等的实数根.
有两个不相等的实数根.
(1)求 的取值范围;
的取值范围;
(2)若 为正整数,且该方程的根都是整数,求
为正整数,且该方程的根都是整数,求 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com