
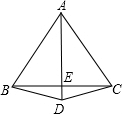
 如图,AB=AC,DB=DC,若∠ABC为60°,BE=3cm,则AB=6cm.
如图,AB=AC,DB=DC,若∠ABC为60°,BE=3cm,则AB=6cm. 分析 首先证明△ABC为等边三角形,然后依据SSS证明△ABD全等△ACD,从而可得到∠BAD=∠CAD,然后依据等腰三角形三线合一的性质可得到BE=CE,从而可求得BC的长,故此可得到AB的长.
解答 解:在△ABD和△ACD中$\left\{\begin{array}{l}{AB=AC}\\{DB=DC}\\{AD=AD}\end{array}\right.$,
∴△ABD≌△ACD.
∴∠BAD=∠CAD.
又∵AB=AC,
∴BE=EC=3cm.
∴BC=6cm.
∵AB=AC,∠BAC=60°,
∴△ABC为等边三角形.
∴AB=6cm.
故答案为:6.
点评 本题主要考查的是等边三角形的性质和判定,等腰三角形的性质、全等三角形的性质和判定,求得BC的长是解题的关键.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:选择题
| A. | a<2 | B. | a=2 | C. | a>2 | D. | a≤2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 鞋店老板比较关心的是一段时间内卖出的鞋的尺码组成的一组数据的众数 | |
| B. | 某种彩票的中奖率是2%,则买50张这种彩票一定会中奖 | |
| C. | 为了了解某品牌灯管的使用寿命,应采用全面调查的方式 | |
| D. | 若甲组数据的方差S${\;}_{甲}^{2}$=0.06,乙组数据的方差S${\;}_{乙}^{2}$=0.1,则乙组数据比甲组数据稳定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
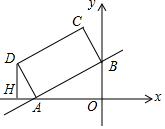 如图,在直角坐标系xOy中,直线y=$\frac{1}{2}$x+2与x轴,y轴分别交于A、B两点,以AB为边在第二象限内作矩形ABCD,使AD=$\sqrt{5}$.
如图,在直角坐标系xOy中,直线y=$\frac{1}{2}$x+2与x轴,y轴分别交于A、B两点,以AB为边在第二象限内作矩形ABCD,使AD=$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -6 | B. | -8 | C. | -12 | D. | -18 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com