
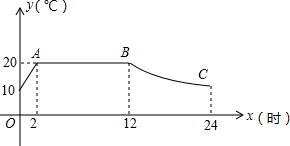
 ij�߲�����������װ�к���ϵͳ�Ĵ�������һ�����������¶�Ϊ15��20�����Ʒ�֣���ͼ��ij�����ϵͳ�ӿ������رռ��رպ������¶�y���棩��ʱ��x��h���仯�ĺ���ͼ������AB���Ǻ��½Σ�BC����˫����y=$\frac{k}{x}$��һ���֣������ͼ����Ϣ����������⣺
ij�߲�����������װ�к���ϵͳ�Ĵ�������һ�����������¶�Ϊ15��20�����Ʒ�֣���ͼ��ij�����ϵͳ�ӿ������رռ��رպ������¶�y���棩��ʱ��x��h���仯�ĺ���ͼ������AB���Ǻ��½Σ�BC����˫����y=$\frac{k}{x}$��һ���֣������ͼ����Ϣ����������⣺���� ��1�����ô���ϵ������һ�κ����뷴������������ʽ���ɣ�
����ͼ��ֱ�ӵó������¶�20���ʱ��Ϊ10-2=8��Сʱ����
��2����x=18���뺯������ʽ���y��ֵ���������жϣ�
��3���۲�ͼ���֪�����κ�������y��15�ĵ㣬����AB���Ǻ��½Σ�y=20�����Լ���AD��BC���ε�y=15ʱ��Ӧ��xֵ��������ǽ��ۣ�
��� �⣺��1����AD����ʽ��y=mx+n��m��0������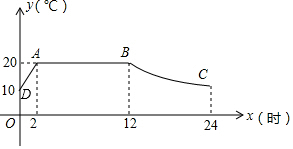 $\left\{\begin{array}{l}{2m+n=20}\\{n=10}\end{array}\right.$��
$\left\{\begin{array}{l}{2m+n=20}\\{n=10}\end{array}\right.$��
���$\left\{\begin{array}{l}{m=5}\\{n=10}\end{array}\right.$��
��y=5x+10��
��˫����y=$\frac{k}{x}$����B��12��20����
��20=$\frac{k}{12}$��
���k=240��
��y=$\frac{240}{x}$��
����������y��x�ĺ�������ʽΪ��y=$\left\{\begin{array}{l}{5x+10��0��x��2��}\\{20��2��x��12��}\\{\frac{240}{x}��12��x��24��}\end{array}\right.$��
��2����x=18ʱ��y=$\frac{240}{18}$=13$\frac{1}{3}$��
����13$\frac{1}{3}$��15��
�ʵ�x=18ʱ�������ڵ��¶Ȳ������˸�Ʒ���߲˵�������
��3����y=15ʱ��15=5x+10��x=1��
15=$\frac{240}{x}$��
���x=16
����16-1=15��
�ʺ���ϵͳ��һ���ڱ��ִ���������������¶���15��Сʱ��
���� �����Ƿ�����������һ�κ������ۺϣ������˷�����������һ�κ��������ʺ�Ӧ�ã�������ʱҪ�����ô���ϵ����ȷ�������Ľ���ʽ���ٹ۲�ͼ���ص㣬��Ϸ�����������һ�κ�������������


 ��ʦ�㾦�ִʾ��ƪϵ�д�
��ʦ�㾦�ִʾ��ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
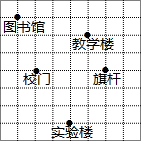 ��ͼ��ijѧУ��ƽ��ʾ��ͼ����8��8�������������У����ʵ��¥����λ�õ�����Ϊ��-2��-4����
��ͼ��ijѧУ��ƽ��ʾ��ͼ����8��8�������������У����ʵ��¥����λ�õ�����Ϊ��-2��-4�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3��$\frac{1}{3}$ | B�� | 2��-$\frac{1}{3}$ | C�� | 3��$\frac{1}{2}$ | D�� | 2��-$\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
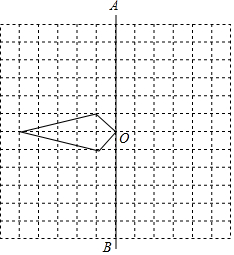 ��ͼ���ڱ߳�Ϊ1����λ���ȵ�С��������ɵ�12��10�ij�������������һ�ı��Σ��������������⣺
��ͼ���ڱ߳�Ϊ1����λ���ȵ�С��������ɵ�12��10�ij�������������һ�ı��Σ��������������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
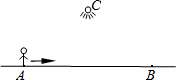 ��ͼ������С���ӵ�A����·��C�����·���ֱ���ߵ���B������Ӱ��y�������A֮��ľ���x�ı仯���仯����ô����ͼ�����ܷ�ӳy��x֮��ĺ�����ϵ���ǣ�������
��ͼ������С���ӵ�A����·��C�����·���ֱ���ߵ���B������Ӱ��y�������A֮��ľ���x�ı仯���仯����ô����ͼ�����ܷ�ӳy��x֮��ĺ�����ϵ���ǣ�������| A�� |  | B�� | 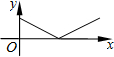 | C�� | 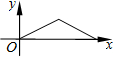 | D�� | 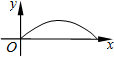 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6 | B�� | $\frac{35}{2}$ | C�� | 20 | D�� | 24 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com