
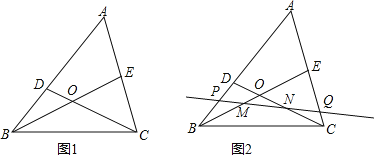
【题目】如图,在![]() 中,D、E分别为AB、AC上的点,线段BE、CD相交于点O,且
中,D、E分别为AB、AC上的点,线段BE、CD相交于点O,且![]() .
.
![]() 求证:
求证: ![]() ∽
∽![]() ;
;
![]() 求证:
求证: ![]() ;
;
![]() 若M、N分别是BE、CD的中点,过MN的直线交AB于P,交AC于Q,线段AP、AQ相等吗?为什么?
若M、N分别是BE、CD的中点,过MN的直线交AB于P,交AC于Q,线段AP、AQ相等吗?为什么?
【答案】(1)证明见解析;(2)证明见解析;(3)![]() ,理由见解析
,理由见解析
【解析】试题分析:(1)根据已知条件得到∠DOB=∠A,由于∠ABE=∠ABE,于是得到结论;
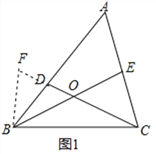
(2)延长CD,在CD延长线上取一点F,使BF=BD,根据等腰三角形的性质得到∠BDF=∠BFD,根据三角形的外角的性质得到∠BDF=∠BEC,于是得到∠BFD=∠BEC,根据全等三角形的性质即可得到结论;
(3)取BC的中点G,连接GM,GN,根据三角形中位线的性质得到GM∥CE,GM=![]() CE,GN∥BD,GN=
CE,GN∥BD,GN=![]() BD,根据平行线的性质得到∠2=∠4,∠3=∠1,等量代换得到∠1=∠2,于是得到AP=AQ.
BD,根据平行线的性质得到∠2=∠4,∠3=∠1,等量代换得到∠1=∠2,于是得到AP=AQ.
试题解析: ![]() 证明:
证明: ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ∽
∽![]() ;
;
![]() 解:延长CD,在CD延长线上取一点F,使
解:延长CD,在CD延长线上取一点F,使![]() ,
,
![]() ,
,
![]() ,
,
由![]() 得
得![]() ,
,
![]() ,
,
![]() ,
,
在![]() 与
与![]() 中,
中, 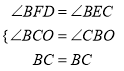 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ;
;
![]() 解:
解: ![]() ,
,

理由:取BC的中点G,连接![]() ,
,
![]() 分别是
分别是![]() 的中点,
的中点,
![]() 是中位线,
是中位线,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.


科目:初中数学 来源: 题型:
【题目】回答下列问题:
(1)如图所示的甲、乙两个平面图形能折什么几何体?
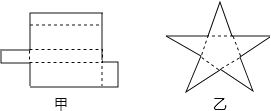
(2)由多个平面围成的几何体叫做多面体.若一个多面体的面数为f,顶点个数为v,棱数为e,分别计算第(1)题中两个多面体的f+v﹣e的值?你发现什么规律?
(3)应用上述规律解决问题:一个多面体的顶点数比面数大8,且有50条棱,求这个几何体的面数.
查看答案和解析>>
科目:初中数学 来源: 题型:
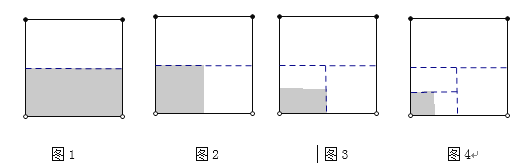
【题目】《庄子·天下》:“一尺之棰,日取其半,万世不竭.”意思是说:一尺长的木棍,每天截掉一半,永远也截不完.我国智慧的古代人在两千多年前就有了数学极限思想,今天我们运用此数学思想研究下列问题.
(规律探索)
(1)如图1所示的是边长为1的正方形,将它剪掉一半,则S阴影1=1-![]() =__________;
=__________;
如图2,在图1的基础上,将阴影部分再裁剪掉—半,则S阴影2=1-![]() -(
-(![]() )2=_______;
)2=_______;
同种操作,如图3,S阴影3=1-![]() -(
-(![]() )2-(
)2-(![]() )3=__________;
)3=__________;
如图4,S阴影4=1-![]() -(
-(![]() )2-(
)2-(![]() )3-(
)3-(![]() )4=___________;
)4=___________;
……
若同种地操作n次,则S阴影n=1-![]() -(
-(![]() )2-(
)2-(![]() )3-…-(
)3-…-(![]() )n=_________.
)n=_________.
(规律归纳)
(2)直接写出![]() +
+![]() +
+![]() +…+
+…+![]() 的化简结果:_________.
的化简结果:_________.
(规律应用)
(3)直接写出算式![]() +
+![]() +
+![]() +…+
+…+![]() 的值:__________.
的值:__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如点M、N把线段AB分割成AM、MN、BN,若以AM、MN、BN,为边的三角形是一个直角三角形,则称点M、N是线段AB的勾股分割点.
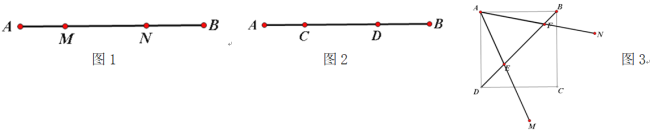
(1)如图2,已知点C、D是线段AB的勾股分割点,若AC=3,DB=4,求CD的长;
(2)如图3,在正方形ABCD中,∠MAM=45°,角的两边AM、AN分别交BD于E、F(不与端点重合),求证:E、F是BD的勾股分割点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图1,AB∥CD, ![]() ,
,![]() .求
.求![]() 度数.
度数.
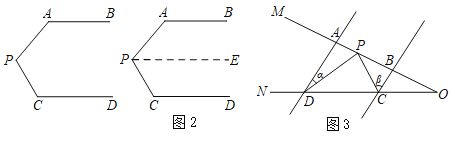
小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可得![]() _______.
_______.
问题迁移:如图3,AD∥BC,点P在射线OM上运动, ![]() ,
, ![]() .
.
(1)当点P在A、B两点之间运动时, ![]() 、
、![]() 、
、![]() 之间有何数量关系?请说明理由.
之间有何数量关系?请说明理由.
(2)如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出![]() 、
、![]() 、
、![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
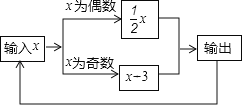
【题目】如图,这是一种数值转换机的运算程序,若第一次输入的数为7,则第2018次输出的数是_____;若第一次输入的数为x,使第2次输出的数也是x,则x=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
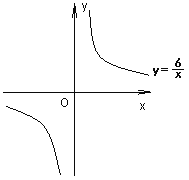
【题目】若反比例函数![]() 与一次函数
与一次函数![]() 的图象都经过点A(
的图象都经过点A(![]() ,2)
,2)
(1)求点A的坐标;
(2)求一次函数![]() 的解析式;
的解析式;
(3)设O为坐标原点,若两个函数图像的另一个交点为B,求△AOB的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019女排世界杯于9月14月至29日在日本举行,赛制为单循环比赛(即每两个队之间比赛一场),一共比赛66场,中国女排以全胜成绩卫冕世界杯冠军,为国庆70周年献上大礼,则中国队在本届世界杯比赛中连胜( )
A.10场B.11场C.12场D.13场
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰三角形ABC中,AB=AC,点D,E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.

(1)求证:∠ABE=∠ACD;
(2)求证:过点A、F的直线垂直平分线段BC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com