
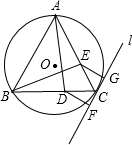
 如图,给定锐角三角形ABC,BC<CA,AD,BE是它的两条高,过点C作△ABC的外接圆的切线l,过点D,E分别作l的垂线,垂足分别为F,G.试比较线段DF和EG的大小,并证明你的结论.
如图,给定锐角三角形ABC,BC<CA,AD,BE是它的两条高,过点C作△ABC的外接圆的切线l,过点D,E分别作l的垂线,垂足分别为F,G.试比较线段DF和EG的大小,并证明你的结论. | DF |
| CD |
| BE |
| AB |
| CE |
| AB |
| AD |
| CD |
| BE |
| CE |
| DF |
| CD |
| BE |
| AB |
| CD |
| AB |
| CE |
| AB |
| AD |
| CD |
| BE |
| CE |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
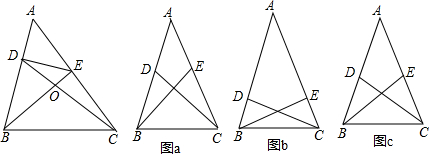
 ∠A,BE与CD相交于点O,探究BD与CE之间的数量关系,并证明你的结论.
∠A,BE与CD相交于点O,探究BD与CE之间的数量关系,并证明你的结论.
查看答案和解析>>
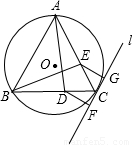
科目:初中数学 来源:2011年全国初中数学竞赛河南赛区预测卷(商丘市外国语中学)(解析版) 题型:解答题
查看答案和解析>>
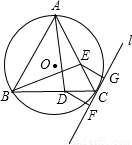
科目:初中数学 来源:2009年全国初中数学竞赛(江西赛区)预赛试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com