
【题目】综合与探究
如图,抛物线y=![]() 与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,连接AC,BC.点P是第四象限内抛物线上的一个动点,点P的横坐标为m,过点P作PM⊥x轴,垂足为点M,PM交BC于点Q,过点P作PE∥AC交x轴于点E,交BC于点F.
与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,连接AC,BC.点P是第四象限内抛物线上的一个动点,点P的横坐标为m,过点P作PM⊥x轴,垂足为点M,PM交BC于点Q,过点P作PE∥AC交x轴于点E,交BC于点F.
(1)求A,B,C三点的坐标;
(2)试探究在点P运动的过程中,是否存在这样的点Q,使得以A,C,Q为顶点的三角形是等腰三角形.若存在,请直接写出此时点Q的坐标;若不存在,请说明理由;
(3)请用含m的代数式表示线段QF的长,并求出m为何值时QF有最大值.

【答案】(1)C(0,﹣4);(2)Q点坐标为(![]() ,
,![]() ﹣4)或(1,﹣3); (3)当m=2时,QF有最大值.
﹣4)或(1,﹣3); (3)当m=2时,QF有最大值.
【解析】
(1)解方程![]() x2
x2![]() x-4=0得A(-3,0),B(4,0),计算自变量为0时的二次函数值得C点坐标;
x-4=0得A(-3,0),B(4,0),计算自变量为0时的二次函数值得C点坐标;
(2)利用勾股定理计算出AC=5,利用待定系数法可求得直线BC的解析式为y=x-4,则可设Q(m,m-4)(0<m<4),讨论:当CQ=CA时,则m2+(m-4+4)2=52,
当AQ=AC时,(m+3)2+(m-4)2=52;当QA=QC时,(m+3)2+(m-4)2=52,然后分别解方程求出m即可得到对应的Q点坐标;
(3)过点F作FG⊥PQ于点G,如图,由△OBC为等腰直角三角形.可判断△FQG为等腰直角三角形,则FG=QG=![]() FQ,再证明△FGP~△AOC得到
FQ,再证明△FGP~△AOC得到![]() ,则PG=
,则PG=![]() FQ,所以PQ=
FQ,所以PQ=![]() FQ,于是得到FQ=
FQ,于是得到FQ=![]() PQ,设P(m,
PQ,设P(m,![]() m2-
m2-![]() m-4)(0<m<4),则Q(m,m-4),利用PQ=-
m-4)(0<m<4),则Q(m,m-4),利用PQ=-![]() m2+
m2+![]() m得到FQ=
m得到FQ=![]() (-
(-![]() m2+
m2+![]() m),然后利用二次函数的性质解决问题.
m),然后利用二次函数的性质解决问题.
(1)当y=0,![]() x2
x2![]() x-4=0,解得x1=-3,x2=4,
x-4=0,解得x1=-3,x2=4,
∴A(-3,0),B(4,0),
当x=0,y=![]() x2
x2![]() x-4=-4,
x-4=-4,
∴C(0,-4);
(2)A=![]() ,
,
易得直线BC的解析式为y=x-4,
设Q(m,m-4)(0<m<4),
当CQ=CA时,m2+(m-4+4)2=52,解得m1=![]() ,m2=-
,m2=-![]() (舍去),此时Q点坐标为(
(舍去),此时Q点坐标为(![]() ,
,![]() -4);
-4);
当AQ=AC时,(m+3)2+(m-4)2=52,解得m1=1,m2=0(舍去),此时Q点坐标为(1,-3);
当QA=QC时,(m+3)2+(m-4)2=52,解得m=![]() (舍去),
(舍去),
综上所述,满足条件的Q点坐标为(![]() ,
,![]() -4)或(1,-3);
-4)或(1,-3);
(3)解:过点F作FG⊥PQ于点G,如图,

则FG∥x轴.由B(4,0),C(0,-4)得△OBC为等腰直角三角形
∴∠OBC=∠QFG=45
∴△FQG为等腰直角三角形,
∴FG=QG=![]() FQ,
FQ,
∵PE∥AC,PG∥CO,
∴∠FPG=∠ACO,
∵∠FGP=∠AOC=90°,
∴△FGP~△AOC.
∴![]() ,即
,即![]() ,
,
∴PG=![]() FG=
FG=![]()
![]() FQ=
FQ=![]() FQ,
FQ,
∴PQ=PG+GQ=![]() FQ+
FQ+![]() FQ=
FQ=![]() FQ,
FQ,
∴FQ=![]() PQ,
PQ,
设P(m,![]() m2-
m2-![]() m-4)(0<m<4),则Q(m,m-4),
m-4)(0<m<4),则Q(m,m-4),
∴PQ=m-4-(![]() m2-
m2-![]() m-4)=-
m-4)=-![]() m2+
m2+![]() m,
m,
∴FQ=![]() (-
(-![]() m2+
m2+![]() m)=-
m)=-![]() (m-2)2+
(m-2)2+![]()
∵-![]() <0,
<0,
∴QF有最大值.
∴当m=2时,QF有最大值.


科目:初中数学 来源: 题型:
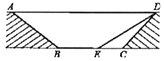
【题目】为缓解交通拥堵,遵义市某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面AD与通道BC平行),通道水平宽度BC为8米,∠BCD=135°,通道斜面CD 的长为6米,通道斜面AB的坡度i=1:![]()
(1)求通道斜面AB的长为多少米;
(2)为增加市民行走的舒适度,拟将设计图中的通道斜面CD的坡度变缓,修改后的通道斜面DE的坡角为30°,求此时BE的长.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,O为直线AB上一点,OC平分∠AOE,∠DOE=90°,则以下结论正确的有____________.(只填序号)
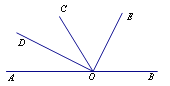
①∠AOD与∠BOE互为余角;
②OD平分∠COA;
③∠BOE=56°40′,则∠COE=61°40′;
④∠BOE=2∠COD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=k1x+b(k1≠0)的图象分别与x轴,y轴相交于点A,B,与反比例函数y2=![]() 的图象相交于点C(﹣4,﹣2),D(2,4).
的图象相交于点C(﹣4,﹣2),D(2,4).
(1)求一次函数和反比例函数的表达式;
(2)当x为何值时,y1>0;
(3)当x为何值时,y1<y2,请直接写出x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年1月20日,山西迎来了“复兴号”列车,与“和谐号”相比,“复兴号”列车时速更快,安全性更好.已知“太原南﹣北京西”全程大约500千米,“复兴号”G92次列车平均每小时比某列“和谐号”列车多行驶40千米,其行驶时间是该列“和谐号”列车行驶时间的![]() (两列车中途停留时间均除外).经查询,“复兴号”G92次列车从太原南到北京西,中途只有石家庄一站,停留10分钟.求乘坐“复兴号”G92次列车从太原南到北京西需要多长时间.
(两列车中途停留时间均除外).经查询,“复兴号”G92次列车从太原南到北京西,中途只有石家庄一站,停留10分钟.求乘坐“复兴号”G92次列车从太原南到北京西需要多长时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明:
已知:如图,AB∥DE,求证:∠D+∠BCD﹣∠B=180°,
证明:过点C作CF∥AB.
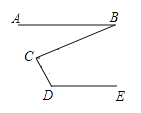
∵AB∥CF(已知),
∴∠B= ( ).
∵AB∥DE,CF∥AB( 已知 ),
∴CF∥DE ( )
∴∠2+ =180° ( )
∵∠2=∠BCD﹣∠1,
∴∠D+∠BCD﹣∠B=180° ( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.
(1)求每套队服和每个足球的价格是多少?
(2)若城区四校联合购买100套队服和a个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用;
(3)假如你是本次购买任务的负责人,你认为到哪家商场购买比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中每个小正方形边长都是1.
(1)画出△ABC关于直线1对称的图形△A1BlCl;
(2)在直线l上找一点P,使PB=PC;(要求在直线1上标出点P的位置)
(3)连接PA、PC,计算四边形PABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,AD是∠BAC的角平分线,DE⊥AB,垂足为点E,DE=1,BE=![]() ,则△ABC的周长是( )
,则△ABC的周长是( )

A.6+![]() B.3+2
B.3+2![]() C.6+2
C.6+2![]() D.3+3
D.3+3![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com