
【题目】如图,已知四边形ABCD是矩形,延长AB至点F,连结CF,使得CF=AF,过点A作AE⊥FC于点E. 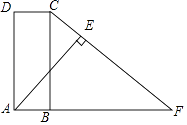
(1)求证:AD=AE.
(2)连结CA,若∠DCA=70°,求∠CAE的度数.
【答案】
(1)证明:连接AC,如图所示:
∵CF=AF,∴∠FCA=∠CAF,
∵四边形ABCD是矩形,∴DC∥AB∴,∠DCA=∠CAF,
∴∠FCA=∠DCA,
∵AE⊥FC,
∴∠CEA=90°,
∴∠CDA=∠CEA=90°,
在△ADC和△CAE 中, 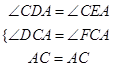 ,
,
∴△ADC≌△CAE (AAS),
∴AD=AE;
(2)解:∵△ADC≌△CAE,
∴∠CAE=∠CAD,
∵四边形ABCD是矩形,
∴∠D=90°,
∴∠CAD=90°﹣∠DCA=90°﹣70°=20°,
∴∠CAE=20°.
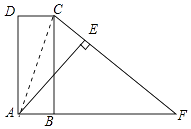
【解析】(1)由等腰三角形的性质和矩形的性质证出∠FCA=∠DCA,由AAS证明△ADC≌△CAE,即可得出结论;(2)由全等三角形的性质得出∠CAE=∠CAD,求出∠CAD=90°﹣∠DCA=20°,即可得出答案.
【考点精析】认真审题,首先需要了解矩形的性质(矩形的四个角都是直角,矩形的对角线相等).


科目:初中数学 来源: 题型:
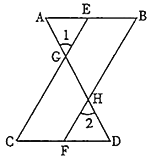
【题目】完成下面的证明:
如图,已知![]() ,
,![]() ,可推得
,可推得![]() .
.
理由如下:∵![]() (已知),
(已知),
且![]() ( )
( )
∴![]() (等量代换)
(等量代换)
∴________∥________( )
∴∠________![]() ( )
( )
又∵![]() (已知)
(已知)
∴![]() ( )
( )
∴![]() ( )
( )
查看答案和解析>>
科目:初中数学 来源: 题型:
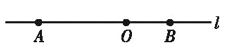
【题目】如图,直线![]() 上有
上有![]() ,
,![]() 两点,
两点,![]() ,
,![]() 是线段
是线段![]() 上的一点,
上的一点,![]() .
.
(1)![]()
![]() ,
,![]()
![]() ;
;
(2)若点![]() 是直线
是直线![]() 上一点,且满足
上一点,且满足![]() ,求
,求![]() 的长;
的长;
(3)若动点![]() ,
,![]() 分别从点
分别从点![]() ,
,![]() 同时出发,向右运动,点
同时出发,向右运动,点![]() 的速度为
的速度为![]() ,点
,点![]() 的速度为
的速度为![]() .设运动时间为
.设运动时间为![]() ,当点
,当点![]() 与点
与点![]() 重合时,
重合时,![]() ,
,![]() 两点停止运动.
两点停止运动.
①当![]() 为何值时,
为何值时,![]() ?
?
②当点![]() 经过点
经过点![]() 时,动点
时,动点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度也向右运动.当点
的速度也向右运动.当点![]() 追上点
追上点![]() 后立即返回,以
后立即返回,以![]() 的速度向点
的速度向点![]() 运动,遇到点
运动,遇到点![]() 后再立即返回,以
后再立即返回,以![]() 的速度向点
的速度向点![]() 运动,如此往返.当点
运动,如此往返.当点![]() 与点
与点![]() 重合时,
重合时,![]() ,
,![]() 两点停止运动,此时点
两点停止运动,此时点![]() 也停止运动.在此过程中,请直接写出点
也停止运动.在此过程中,请直接写出点![]() 运动的总路程.
运动的总路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“重百”、“沃尔玛”两家超市出售同样的保温壶和水杯,保温壶和水杯在两家超市的售价分别一样.已知买1个保温壶和1个水杯要花费60元,买2个保温壶和3个水杯要花费130元.
(1)请问:一个保温壶与一个水杯售价各是多少元;(列方程组求解)
(2)为了迎接“五一劳动节”,两家超市都在搞促销活动,“重百”超市规定:这两种商品都打九折;“沃尔玛”超市规定:买一个保温壶赠送一个水杯.若某单位想要买4个保温壶和15个水杯,如果只能在一家超市购买,请问选择哪家超市购买更合算,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
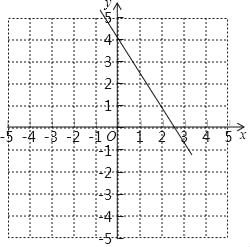
【题目】点A(0,4),B(2,1)是直角坐标系中的两个点.
(1)请在平面直角坐标系中描出A,B两点,并画出直线AB;
(2)写出B点关于y轴的对称点B′的坐标 ;
(3)求出直线AB与x轴的交点坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则点B3的坐标是_____;点B2018的坐标是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读:对于函数y=ax2+bx+c(a≠0),当t1≤x≤t2时,求y的最值时,主要取决于对称轴x=﹣ ![]() 是否在t1≤x≤t2的范围和a的正负:①当对称轴x=﹣
是否在t1≤x≤t2的范围和a的正负:①当对称轴x=﹣ ![]() 在t1≤x≤t2之内且a>0时,则x=﹣
在t1≤x≤t2之内且a>0时,则x=﹣ ![]() 时y有最小值,x=t1或x=t2时y有最大值;②当对称轴x=﹣
时y有最小值,x=t1或x=t2时y有最大值;②当对称轴x=﹣ ![]() 在t1≤x≤t2之内且a<0时,则x=﹣
在t1≤x≤t2之内且a<0时,则x=﹣ ![]() 时y有最大值,x=t1或x=t2时y有最小值;③当对称轴x=﹣
时y有最大值,x=t1或x=t2时y有最小值;③当对称轴x=﹣ ![]() 不在t1≤x≤t2之内,则函数在x=t1或x=t2时y有最值.
不在t1≤x≤t2之内,则函数在x=t1或x=t2时y有最值.
解决问题:
设二次函数y1=a(x﹣2)2+c(a≠0)的图象与y轴的交点为(0,1),且2a+c=0.
(1)求a、c的值;
(2)当﹣2≤x≤1时,直接写出函数的最大值和最小值;
(3)对于任意实数k,规定:当﹣2≤x≤1时,关于x的函数y2=y1﹣kx的最小值称为k的“特别值”,记作g(k),求g(k)的解析式;
(4)在(3)的条件下,当“特别值”g(k)=1时,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com